Cat on a Wall
How high is the wall that this cat is lying on?
Problem
A cat lies on top of a low wall and looks up towards the birds in the top of a tree. There is a bush between the cat and the tree, and the cat can only just see over the top of the bush.
The bush is a horizontal distance of H metres from the wall, and the tree is a horizontal distance of H metres from the bush.
The height of the bush is 4 m. The height of the tree is 7 m.
How high is the wall?
This problem is adapted from the World Mathematics Championships
Student Solutions
It is helpful to draw a simple diagram of the situation.
We assume that the cat's eye is at the same height as the top of the wall. The blue line show's the cat's line of vision as it looks over the bush at the tree.

Consider the pink triangles on the diagram below. Their sloped sides are along the same straight line (the blue line). So they both have the same slope, or gradient - and make the same angle with the bases of the triangles.
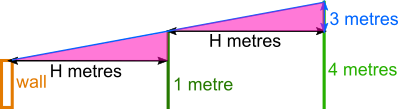
They also have the same base, H metres, and are both right-angled.
So they share a base and the two angles on either sides of it - which means that they are congruent.
The tree is 3 metres taller than the bush, so the vertical side of the pink triangle between the bush and the tree is 3 metres.
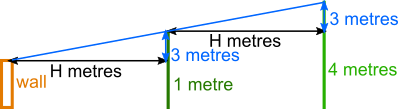
That means that the vertical side of the triangle between the wall and the bush is also 3 metres.
So, since the bush is 4 metres tall, the wall must be only 1 metre high.
