Doubly Isosceles
Find the missing distance in this diagram with two isosceles triangles
Problem
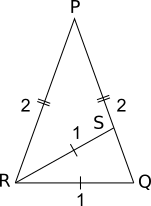
Triangle PQR is isosceles, with PQ = PR = 2.
Triangle QRS is isosceles, with QR = RS = 1.
Find the length QS.
This problem is taken from the World Mathematics Championships
Student Solutions

It is helpful to find what these two triangles have in common. Angle PQR (or SQR), shown in red on the right, is an angle in both triangles.
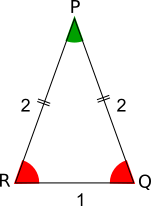
Triangle PQR is isosceles, so angle PRQ is equal to angle PQR. It is also shown in red in the diagram on the left.
The green angle at P is the angle that needs to be added to two red angles to make 180$^\circ$.
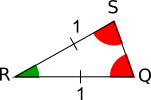
Triangle QRS is also isosceles, and its line of symmetry is through R. So angle RSQ is equal to angle SQR. It is also shown in red in the diagram on the right.
The angle at R also makes a sum of 180$^\circ$ when added to the two red angles. So it is equal to the green angle at P.
But this means that the triangles PQR and QRS are similar.
We can use either that the scale factor between triangle QRS and triangle PQR is 2 (shown below in the diagram on the left), or that the ratio between the longer sides and the shorter side of each triangle is 1:2 (shown below in the diagram on the right).

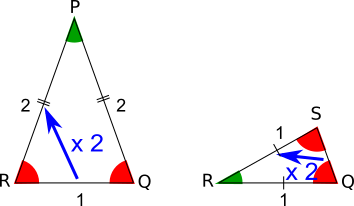
Either of these facts about similar triangles tell us that QS = $\frac12$.
