Order the Products
Can you put these products in order of size?
Problem
Without calculating the five products below, put them in order of size, from smallest to largest.
| 210$\times$190 | 198$\times$202 | 200$\times$200 |
| 195$\times$205 | 186$\times$214 |
This problem is taken from the World Mathematics Championships
Student Solutions
Answer:
186$\times$214 (smallest)
210$\times$190
195$\times$205
198$\times$202
200$\times$200 (largest)
Numerically, using 200$\times$200
210$\times$190 = (200 + 10)(200 $-$ 10) = 200$^2$ + 2000 $-$ 2000 $-$ 100
= 200$^2-$ 100
195$\times$205 = (200 $-$ 5)(200 + 5) = 200$^2$ $-$ 1000 + 1000 $-$ 25
= 200$^2-$ 25
198$\times$202 = (200 + 2)(200 $-$ 2) = 200$^2-$ 4
186$\times$214 = (200 + 14)(200 $-$ 14) = 200$^2-$ 14$^2$
$\therefore$ 186$\times$214 $\lt$ 210$\times$190 $\lt$ 195$\times$205 $\lt$ 198$\times$202 $\lt$ 200$\times$200
Writing the numbers in terms of 200
All of the products are $(200 +n)(200 -n)$ for some small value of $n$.
$\begin{align}(200+n)(200-n)&=200^2+200n-200n-n^2\\
&=200^2-n^2\end{align}$
$n$ larger $\Rightarrow200^2-n^2$ smaller (for $n\gt0$).
$\therefore$ 186$\times$214 $\lt$ 210$\times$190 $\lt$ 195$\times$205 $\lt$ 198$\times$202 $\lt$ 200$\times$200
Diagrammatic representation
Red strip and green strip both have width $1$, area $200$
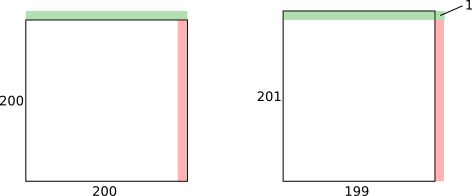
Red strip and green strip both have width $n$, area $200n$

