Packing Small Boxes
How many small boxes will fit inside the big box?
Problem
A large box measures 1.7 m by 1.2 m by 1.5 m.
It is to be packed with smaller boxes each measuring 15 cm by 20 cm by 20 cm.
What is the greatest number of small boxes that can be fitted into the larger box, assuming that they are all placed in the same orientation?
This problem is taken from the World Mathematics Championships
Student Solutions
If the small boxes are all packed in the same orientation, then the total number of boxes can be found by multiplying the number of boxes stacked along each edge. This is shown (with arbitrarily sized boxes) on the diagram below, where the large box contains 48 smaller boxes in this orientation:
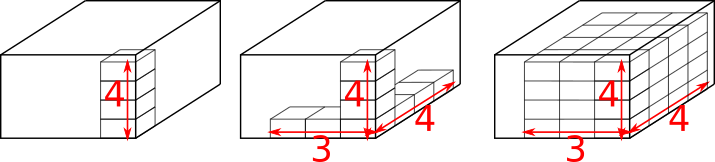
To choose the best orientation for the small boxes, we should consider how many small boxes would fit along each edge of the large box the different ways round. The less unused space, the better!
1.2 m = 120 cm, which is equal to:
- 8$\times$15, so this side could be made up of 8 boxes stacked along their 15 cm edges
- 6$\times$20, so it could also be 6 boxes stacked along their 20 cm edges
1.5 m = 150 cm, which is equal to:
- 10$\times$15, so this could be 10 boxes stacked along their 15 cm edges
- 7$\times$20 + 10, so it could also be 20 boxes stacked along their 20 cm edges with 10 cm left over
1.7 m = 170 cm, which is equal to:
- 8$\times$20 + 10 (8 boxes along their 20 cm edges, with 10 cm left over)
- 11$\times$15 + 5 (11 boxes along their 15 cm edges, with 5 cm left over)
- 10$\times$15 + 1$\times$20 (10 boxes along their 15 cm edges, and 1 box along its 20 cm edge)
- 7$\times$20 + 2$\times$15 (7 boxes along their 20 cm edges and 2 boxes along their 15 cm edges)
If all of the small boxes are in the same orientation, then the best option appears to be 6$\times$20 for 120, 10$\times$15 for 150, which leaves 8$\times$20 + 10 for 170 (remember that the boxes only have one 15 cm edge but they have two 20 cm edges!). That would give us a total of 6$\times$10$\times$8 = 480 little boxes.
