Small Groups
Suppose you go to sleep with your T-shirt on, get hot in the night and take it off, then later in the dark put it back on. How might you be wearing your T-shirt in the morning? In your sleepy state you might have turned it inside out, or back to front, or back to front and inside out, or left it the same way as before. These are four different actions on your T-shirt. You could have done this several times, combining any of the four different actions. Of course any of the actions is reversible in the sense that you can end up with the T-shirt the same way as at the start.
We are going to be mathematical about this and use symbols and a table to sum up how the actions can be combined. We use S to mean put the T-shirt on the same way as before, however it was, B to mean turn it back to front, O to mean turn it inside out, and A to mean turn it inside out and back to front. Note that these letters don't describe the end result because that depends on the way you were wearing the T-shirt in the first place, only on how the actions affected it. For example if the first time you turned it back to front and inside out (A), and the second time just turned it inside out (O), then combining these two actions (O*A) would be the same as a single action of turning it back to front (O*A = B). Now complete the table before reading on. Apply S, B, O or A in the column first.
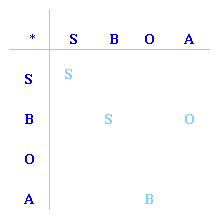
Here we have a set of actions and a rule for combining them, where combining two actions gives another action in the set, we have an 'identity' S, and each action combined with itself gives S. This is a group of 4 elements. Groups are very important in mathematics, they are used to solve many problems, and some people spend their whole lives studying groups and finding out new things about them.
This article will give an account of all possible groups of one, two, three and four elements, but first think about a group you already know well, without perhaps ever calling it a group. The integers with the operation of addition form a group. Perhaps we should not even mention this group in an article called "Small Groups" because it has infinitely many members, but it is a free country! When we add two integers we always get another integer. Like our T-shirt actions, this group has an identity. Zero is the identity because 0 + N = N for any integer N. If we take any integer N then there is another integer -N so that when we add N and -N we get the identity. Elements which combine to give the identity are called inverses, for example 6 + (-6) = 0, 159 + (-159) = 0 etc. In our T-shirt group each action is its own inverse so the actions are called self inverse.
Modulus arithmetic provides lots of examples of small groups. Take the set of numbers {1, 3, 5, 7} and fill out the multiplication table below modulo 8; that is multiply the numbers together, divide by 8 and write down the remainder.
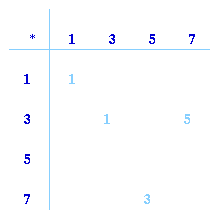
What do you notice about the table when you have completed it?
Did you notice that no other numbers apart from 1, 3, 5 and 7 are needed to complete the table? What else did you notice? The identity is 1 and the elements are all self inverse. Each row has all the numbers 1, 3, 5 and 7 once only and in a different order. The same is true for the columns. Again this is a group of 4 elements.
Now consider four actions on a rectangle together with combinations of these actions. These actions are I, X, Y and H where I is the identity, X is a flip about the horizontal line turning the rectangle over, Y is a flip about the vertical line, turning the rectangle over and H is a half turn about the centre O. After any of these actions the rectangle goes back into exactly the same space. Now make up your own table.
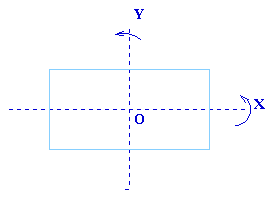
Compare your table with the two previous tables. What do you notice?
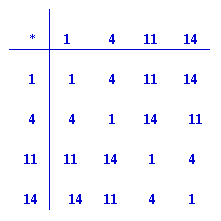
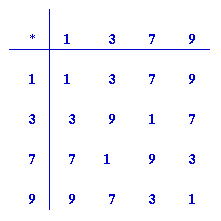
Did you notice the essential difference? This time only 9 is self inverse, and 3 and 7 are inverses of each other. This is a group but it is not the Klein 4-group. We don't get 3 times 3 to be the identity so what happens to powers of 3? The powers of 3 modulo 10 give all the elements of the group:
Now suppose four people sit around a table in a Chinese restaurant, very hungry, but there is only one dish on the lazy-susan in the middle of the table.

There are 4 actions on the lazy-susan which put the dish in front of the four people so they can serve themselves, a quarter turn, a half turn, a three quarter turn and a whole turn. Clearly we can call these actions Q, Q ², Q ³ and Q4 = I, because two quarter turns make a half turn, and four quarter turns make a whole turn but that is equivalent to returning the lazy-susan to its starting position. The group table is:
| * | I | Q | Q ² | Q ³ |
| ---------------------- | ||||
| I | I | Q | Q ² | Q ³ |
| Q | Q | Q ² | Q ³ | I |
| Q ² | Q ² | Q ³ | I | Q |
| Q ³ | Q ³ | I | Q | Q ² |
This is what is called the C4 group, or cyclic group with 4 elements. The fact that taking powers of 3 modulo 10 gives all the elements 1, 3, 7 and 9 suggests that this modular group is also cyclic. The 'powers of 3 modulo 10' group and the 'lazy-susan' group have exactly the same structure, which is easily checked by replacing 1 by I, 3 by Q, 7 by Q ³ and 9 by Q ² . They are both the group C4 . Although there are many different contexts in which they can arise, there are only two possible groups with four elements, the Klein 4-group and C4 . Reason?
There is a group with just one element containing the identity all on its own. With two elements there has to be the identity and a self inverse element and we have already seen groups with two elements buried in the groups we have been exploring (subgroups). Take S and B in the T shirt group, I and H in the rectangles group, I and Q ² in the lazy-susan group; each of these gives a group with two elements. Two more examples groups are given by "putting on your glasses" and "putting on some rubber gloves to do the washing up". The reader is left to decide how many elements these groups have.
With three elements there is only one possible structure Reason? . Suppose we had three diners in the Chinese restaurant equally spaced around a circular table, now they would have to turn the lazy-susan through 120o , 240o or 360o to get that delicious dish of mouth watering food in front of each of them. We denote the three actions by R, R ² and R ³= I. This gives the following group table for C3 , the cyclic group with three elements.
| * | I | R | R ² | |
| ---------------------- | ||||
| I | I | R | R ² | |
| R | R | R ² | I | |
| R ² | R ² | I | R | |
We can draw networks to represent these groups. Each line in the network represents one of the actions of the group and the vertices show the combinations of the elements.
Image
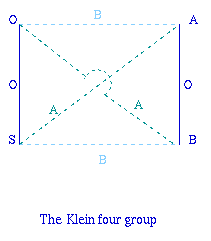
|
Image
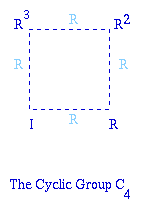
|
You have now met all possible groups with up to four elements. You may like to look at three more modular groups and decide for yourself which types they are.
(a) {1, 2, 3, 4} with multiplication modulo 5
(b) {1, 5, 7, 11} with multiplication modulo 12
(c) {0, 1, 2, 3} with addition modulo 4.
Answers .
