What distance?
Can you use addition and subtraction to answer these questions about real-life distances?
Problem
What Distance? printable sheet
Here are the distances (as the crow flies) in kilometres from London to various cities in the world:
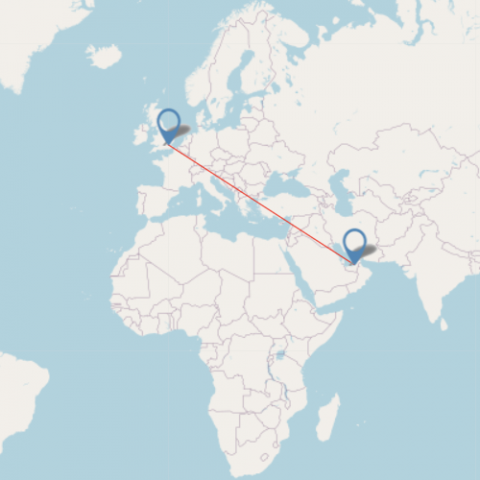
Abu Dhabi 5480 Image
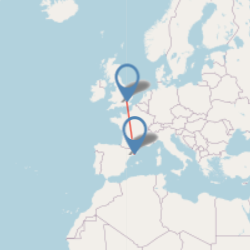
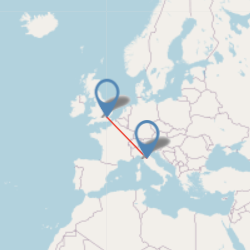
| Barcelona 1139 Image
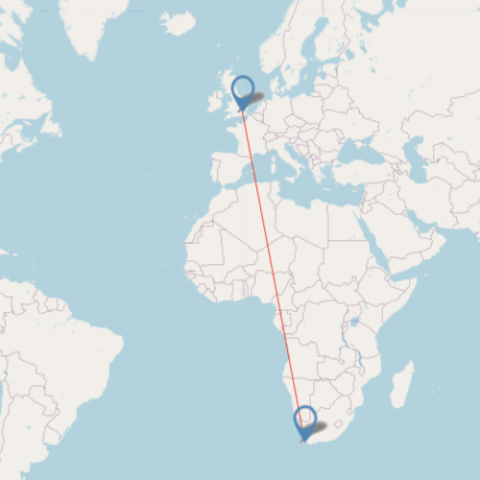
| Cape Town 9680 Image
|
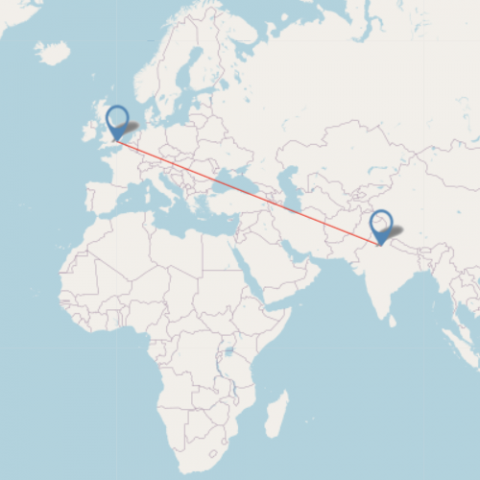
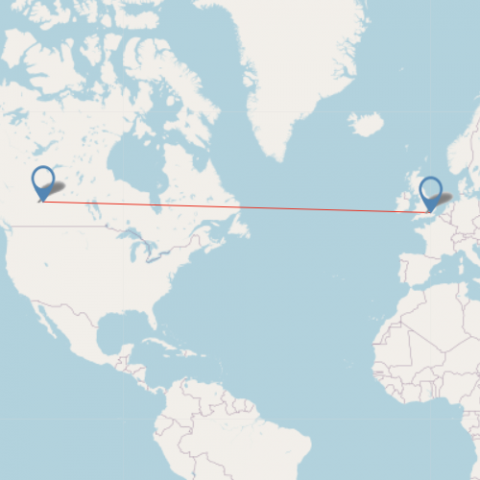
New Delhi 6718 Image
| Edmonton 6805 Image
| Florence 1209 Image
|
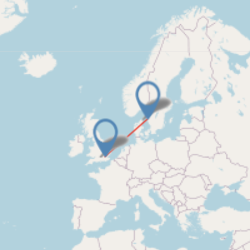
Gothenburg 1039 Image
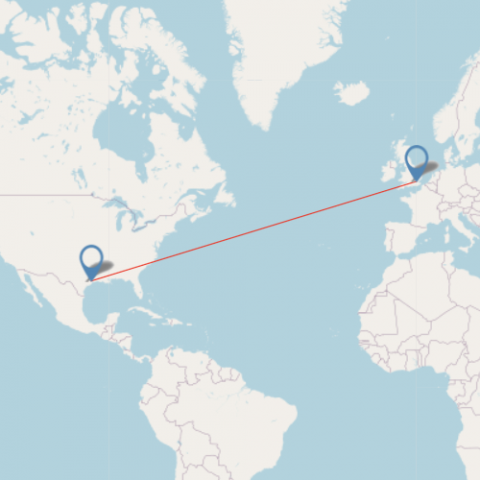
| Houston 7812 Image
| Istanbul 2501 Image
|
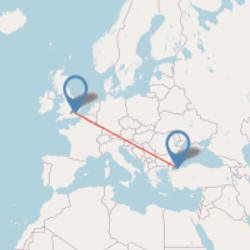
Jerusalem 3611 Image
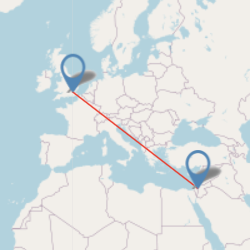
| Karachi 6314 Image
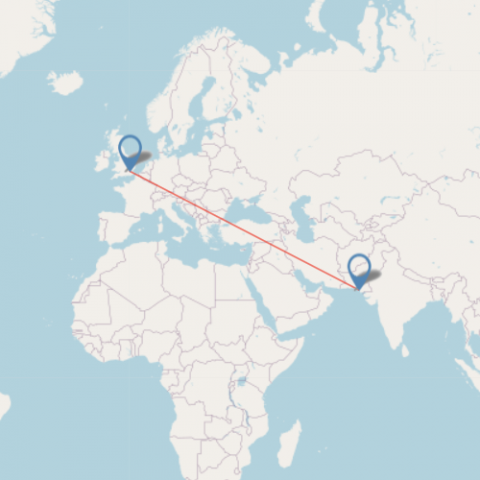
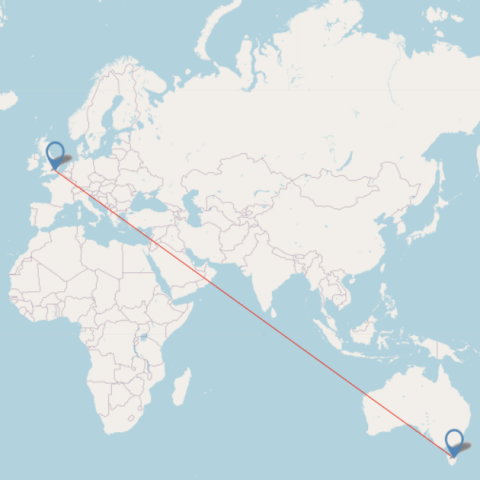
| Launceston 17425 Image
|
Challenge 1
Once you have travelled the first 1000km, how much further will you have to go for each of the twelve journeys?
Rather than actually performing each calculation, could you say which you think will be the most difficult and which will be the easiest, and why?
Now create some similar questions of your own.
Challenge 2
The distance from Copenhagen to London is approximately 1000km. If you always start at Copenhagen before travelling to London for all of the journeys shown above, how far would you travel in each case?
Student Solutions
We were sent in a few ideas about this task. Oliver from Coddington C of E Primary School in England explained which calculations looked easiest and hardest:
I think that Gothenburg will be the easiest because you are only taking off the one and the zero, which is relatively easy.
I think Launceston is the hardest one to work out because it is the biggest number and the biggest calculation.
Fin from Springvale Primary in England thought about subtracting 100km from each distance as well as 1000km:
We noticed that when you travelled 1000 km in, the only digit that changed was the thousands digit and it went down by one. We also tried the hundreds column. Launceston was hard because it had a ten thousand column. When we did the hundreds Gothenburg was hard because the hundreds column was a zero so we had to use the thousands column too.
When we added the extra distance the same thing happened but the digit went up not down.
Joe from Millhouse Primary in England also had similar ideas, and wrote some new questions:
I noticed that it was easy because it was just taking one away from the thousands column.
The easiest was Istanbul because everyone can do 2-1.
I recognised Launceston was the hardest because it isn't just taking one away from the first column it is taking away from the second.
Here are some examples of similar questions I came up with:
If I was travelling to Launceston and someone took me 10,000km how many km would there be left with?
If I was traveling to Istanbul and somebody took me 2,000km how many would I have left?
We also thought if someone had taken us 100km away you take away one from the hundreds column.
Thank you all for sharing your thoughts with us!
Teachers' Resources
Why do this problem?
This simple challenge offers pupils the chance to find 1000 more or less than a given number.
Possible approach
You could show the map images with the associated numbers and invite children to suggest what the numbers mean. (This may provoke a discussion about how miles related to kilometres!)
Then set learners off on the challenges. You could suggest that, rather than attempting all of the calculations, pairs could decide which they think would be the easiest to work out and which would be the hardest, and why.
After a suitable period of time, you could invite pairs to join with another pair and compare their thoughts. If pairs do not agree on which is the easiest/hardest, challenge them to try to persuade the other pair that their 'ranking' is better. This will require knowledge of a range of calculation methods and sound reasoning.
Key questions
How did you work this out?
If you wrote it down to work it out can you show me and talk me through it?
Possible extension
Pupils could work in pairs to write their own similar questions, perhaps investigating the distances from London to other cities.
Possible support
Some pupils may need help with focusing on each particular map and the names that may be unusual for them.
