Where Do We Get Our Feet Wet?
How many high points, low points and passes are there on the island of Crete? I do not know...but I do know a formula which given the number of high points and the number of low points tells me the number of passes. Can you discover it?
I shall end this article by showing how to find the formula, but first I would like to explain how mathematicians think about high points, low points and passes.
It is foolish to hope to go walking across a country (at least in a rainy country like Britain) without getting your feet wet. The lowest point of any piece of country is obviously likely to be wet (indeed such a low point is often marked by a lake). However, it is rather disappointing when having climbed to the highest point you find that the ground is marshy and your feet still get wet.
This sense of unfairness is somewhat reduced when we realise what highest and lowest points have in common -- they are points where the ground is flat. If you are on the side of a hill then the ground slopes upward towards the top of the hill and downward towards the the bottom. Suppose now you stand at the top of the hill. Obviously you can not be facing an upward slope since there is nothing above you. But suppose you were facing a downward slope. In that case by turning round you would face an upward slope which we have already decided is impossible. Since you cannot face an upward or a downward slope you must be standing on flat ground. Where the ground is flat, the water finds it hard to drain away so, naturally, the ground is marshy and your feet get wet.
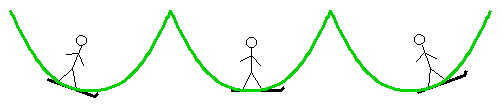
At first sight this sounds paradoxical but my readers may be less unhappy with the conclusion when they have considered the pictures below of a stick man skiing over a two-dimensional hill. The reader must surely agree that at the top of the hill his skis do not point uphill or downhill and so must be flat.

Exactly similar arguments illustrated by similar pictures show that at a lowest point the ground is flat.
Are there any other natural features of the landscape where we may expect to get our feet wet, that is, where the ground is flat? Before trying to answer this question we need to think a bit about the meaning of the word "natural". Consider the two-dimensional hill below. At the point B the ground is flat but the flatness is in some sense artificial since after a small two-dimensional earthquake we get a new hill which has no flat ground anywhere near B . On the other hand the highest point A is a point of natural flatness since after a small earthquake the hill will still have a highest point A' somewhere near A so, although the "point of flatness" may have moved a bit it has not disappeared.
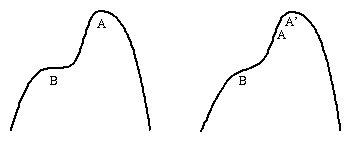
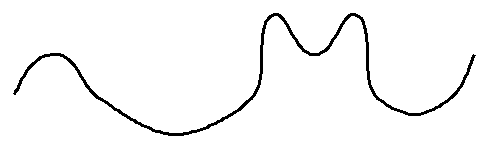
A little experimentation convinces us that the only natural points of flatness for two-dimensional hills are the highest and lowest points (peaks and pits). Moreover, between any two peaks there is a pit and between any two pits there is a peak as shown below.
What happens when we think about a real three-dimensional landscape? Are there any natural points of flatness apart from peaks and pits? I ask the reader to think about this problem before continuing.....
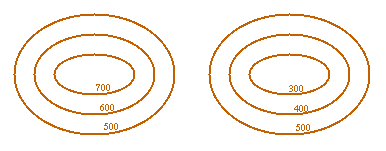
Our first problem is that we are not good at three dimensional drawings. To get round this we use contours. Here are two contour maps of a peak and a pit. The reader is invited to consider a stick man standing on the peak or in the pit and recall the argument showing that the ground here is flat.
Remarkably there are other natural points of flatness. Consider the pass drawn below between two mountains A and B joining two valleys X and Y .
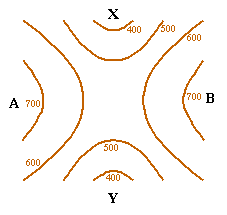
Valley folk toiling over the pass from X to Y will see the pass as a highest point at which their ascending path becomes flat before starting to descend. Mountaineers taking a path from A to B will see the pass as a lowest point at which their descending path becomes becomes flat before starting to ascend. Some paths crossing the pass find it to be a flat high point and others a flat low point but all paths have it as a flat point. We expect passes to be marshy and any experienced hill walker will confirm this to be true.
Are passes 'natural features'? The fact that there are so many of them indicates that they must be. To see that they are, consider the pass drawn above.
If we alter the landscape a bit it will not remove the mountains A and B or the valleys X and Y so the pass must remain. Thus we have three natural kinds of flat points:-- peaks, pits and passes. It is not hard to convince oneself (though we need much more precise definitions before we can think in terms of proof) that these are are the only natural kinds of flat points in three dimensions.
Suppose we have a dry globe like the moon. There is a remarkable relation between the number a of passes, i of pits and e of peaks on that globe. The proof has a pleasantly science fiction quality about it since we imagine ourselves in possession of vast technological resources. First observe that by digging the pits deeper and raising the peaks we can ensure that all the peaks are substantially higher than any of the passes and all the pits are substantially lower than any of the passes. We also make sure that all the passes have different heights.
We now cause rain to fall over the whole of the globe. After a little while there will be i seas (corresponding to the i pits), a passes and 1 connected piece of dry land (continent).
We ensure that the level of water in each lake is the same. As the water level rises the passes will disappear one by one. When a pass disappears one of two things will happen. In the first case two seas will coalesce two form one as shown in the next diagram.

In the second case two arms of the same seas will join to produce a new continent (connected piece of dry land).
In both cases:
remains constant (since in the first case the number of passes P and the number of seas S both decrease by 1, and in the second case the number of passes P decreases by 1 and the number C of continents increases by 1.).
We have thus shown that C + P - S is constant. But we began with C = 1 P = a and S = i so:
Eventually the water level rises to the point where all the passes have disappeared (so P = 0). There will then only be 1 sea (so S =1) and each peak will be the highest point of a separate continent (so C = e ). Thus:
and so a = e + i - 2. In other words we have shown that for any dry globe
Exercise for the reader Show that for an island (like the mainland of Britain or Australia)
I first read this argument in Polya's beautiful book Induction and Analogy in Mathematics . (It is Example 28 in Chapter 9.)
Readers of this article will be pleased to know that they can enjoy more of Tom Korner's writing in:
'Pleasures of Counting' by Dr Tom Korner, published by Cambridge University Press, 1996.
ISBN 0521 568234 ( £ 18.99 paperback)
