Dolly Dolphin
Can you find Dolly Dolphin's average speed as she swims with and against the current?
Problem
Dolly Dolphin swims at a constant speed. When she swims against a current of 2m/s, she travels at 6 m/s.
Dolly swims upstream in this current for 2 minutes, then turns round and swims back to her starting point. What is her average speed?
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: 7.5 m/s
Using the speed-distance-time relationship
2 minutes = 120 seconds at 6 metres/second, Dolly swims 120$\times$6 = 720 metres.
Against 2 m/s current: 6 m/s
No current: 8 m/s
With 2 m/s current: 10 m/s
Travelling 720 metres at 10 m/s will take 72 seconds.
Total distance: 720 + 720 = 1440 metres
Total time: 120 + 72 = 192 seconds.
Average speed of 1440 $\div$ 192 = 360 $\div$ 48 = 45 $\div$ 6 = 7.5 m/s.
Swimming 30 metres each way
Against 2 m/s current: 6 m/s
No current: 8 m/s
With 2 m/s current: 10 m/s
30 metres is a multiple of 6 metres and of 10 metres
30 = 6$\times$5 so 30 metres takes 5 seconds on the way
30 = 3$\times$10 so 30 metres takes 3 seconds on the way back
Total 60 metres takes 8 seconds so average speed is 60$\div$8 = 7.5
Using a graph
Green: upstream, 6 m/s
Red: downstream, 10 m/s
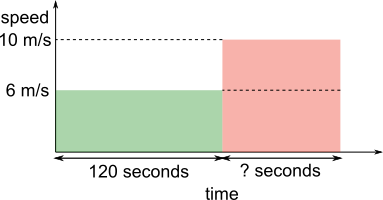
On a speed-time graph, the area represents the distance travelled
Green area + Red area = total distance travelled.
On the two graphs below, the difference between the heights is split into two parts.
The yellow rectangle is moved and reshaped into the first 120 seconds without changing the area and the heights are the same. This represents finding the average speed, because now the same distance is travelled in the same amount of time, but without changing speed.

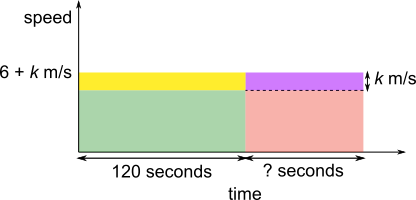
The two yellow rectangles are equal in area, and have bases 120 and ?.
The red and green rectangles in the first diagram are also equal in area with bases 120 and ?.
So the ratio between the heights of the yellow rectangles must be the same as the ratio between the heights of the green and red rectangles.
So $k:4-k$ is equivalent to $6:10$
$k+4-k=4$ and $6+10=16$, so since $16$ is $4$ times bigger than $4$, everything in the ratio $6:10$ is $4$ times bigger than everything in the ratio $k:4-k$.
So $k=6\div4=1.5$, and so the average speed is $6+1.5=7.5$ m/s.
