Add All the Angles
Find the sum of all of the angles denoted by letters in this diagram
Problem
Each letter in this diagram represents the angle between the two lines framing it.
What is the sum of all of the angles denoted by letters?
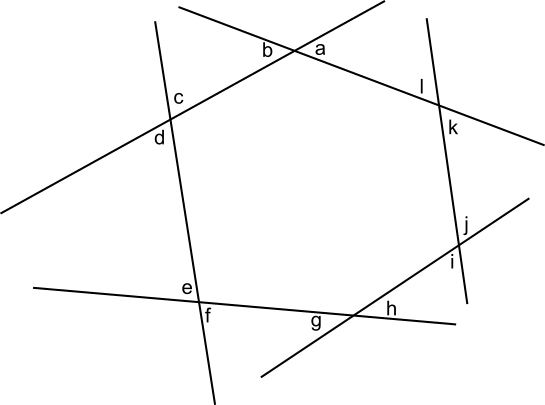
This problem is adapted from the World Mathematics Championships
Student Solutions
Using interior angles of triangles
In the diagram below, all of the lines have been extended so that they cross.
b, c and the red angle form a triangle so add up to 180$^\text o$.
The same is true of f, g and the pink angle and of j, k and the orange angle.
So adding up all of the angles in all 3 triangles gives
b + c + red angle + f + g + pink angle + j + k + orange angle = 180$^\text o$ + 180$^\text o$ + 180$^\text o$
But the red angle, the pink angle and the orange angle are also the angles of a large triangle. So they also add up to 180$^\text o$.
That leaves b + c + f + g + j + k = 180$^\text o$ + 180$^\text o$ = 360$^\text o$.

Using the diagram below in the same way, l + a + d + e + h + i is also equal to 360$^\text o$.

So the sum of all of the angles denoted by letters is 360$^\text o$ + 360$^\text o$ = 720$^\text o$.
Using the exterior angles of hexagons

Imagine walking clockwise around the hexagon shown in red in the diagram on the right. The angles a, k, i, g, e and c are the angles that you would need to turn through to be facing in the direction of the next side.
By the time you got back to where you started from, you would be facing the same way you were facing when you started. So you would have turned through 360$^\text o$.
So a + k + i + g + e + c = 360$^\text o$.

Similarly,
b + d + f + h + j + l = 360$^\text o$.
So the sum of all of the angles denoted by letters is
360$^\text o$ + 360$^\text o$ = 720$^\text o$.
