Zooming in on the Squares

Image

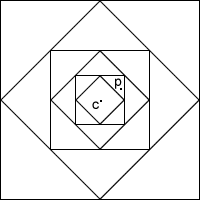
If you start with a large square and join the midpoints of its sides, you will see four right angled triangles. If you remove these four triangles, a second square is left. If you perform the same operation in the second square, a third square is left.

Now perform the operation in the third square and so on and on. What happens?

If you start to do this, after not so many steps, the remaining portion is not recognisable because your pencil lines are too thick to give a clear shape. You could perhaps sharpen your pencil and get out a magnifying glass, but that only lets you observe a few more stages. Then you recognise that the problem is one you can think about but not perform.

Image

You may think about a sequence of smaller and smaller squares, or you may think about the areas. If the area of the original square is $1$ square unit, what is the area of the next square ... and the next and the next?

Either way you get an actual square with an area at every stage.

Some people like to think of the triangles removed (or folded over), and to add their areas together, to see how much area has been cut off at each stage. This gives

$\frac{1}{2}$, $\frac{1}{2}+ \frac{1}{4}$, $\frac{1}{2}+ \frac{1}{4} + \frac{1}{8}$ , ...

Can we think about what happens eventually, or ultimately? Is there a destination which is being approached? If you think of the process happening in time, then there is no 'ultimately', but what is happening is something you imagine, and you can imagine 'ultimately'.

Here are some suggestions as to what might be 'ultimately' left:

(i) nothing,

(ii) a point,

(iii) a square point,

(iv) a small square.

The sequence of numbers giving the area of the square seems to be getting closer to $0$, which gives a reason for saying that no area is ultimately left. Likewise the sequence of numbers giving the total area of the triangles removed seems to tend to $1$. But a single point has no area either. What is a single point? Does it have shape, or only position? Is there perhaps a small square left - during the process a square is left at each stage.

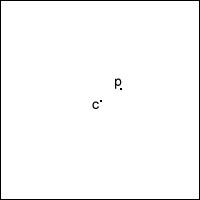
Is the point at the centre of the square ever touched by the cutting off triangles? If not we have no reason to suggest that it is ever removed.

Might any other point be left alone by the cutting off the triangles? Can we be sure that every other point IS removed?

You might also like to think about the lengths of successive diagonals.

If the centre point of the square is C, and any other point is called P, because C is different from P, the distance CP is not 0. This means that the diagonals of the squares remaining eventually shrink to a size less than CP, and the point P is removed.

Image

Image

So every point other than C is removed, so ultimately only C is left and the point C is the limit of the process.

You might like to look at the problem Inside Seven Squares .