Geometry and Gravity 2
This is the second article written for the Summer 1997 NRICH Online Maths Video-conference linking schools in London and Norfolk. This article discusses some possible answers to some of the problems posed in the article "Geometry and Gravity 1".
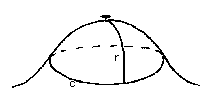
1. Question on curvature
|
|
Positive curvature : | $C < 2 \pi r$ | |
| Flat : | $C = 2 \pi r$ | ||
| Negative curvature : | $C > 2 \pi r$ | ||
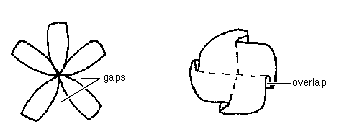
| Positive curvature : | more gap than overlap | ||
| Flat : | equal amounts | ||
| Negative curvature : | less gap than overlap. | ||
2. Task with geodesics
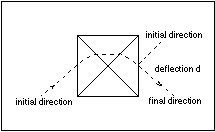
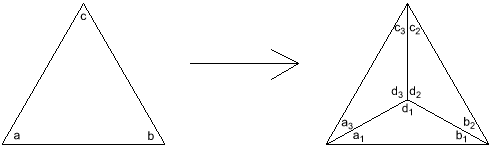
The diagram depicts a tabletop viewed from above on which there is a pyramid with a square base. The geodesic starts on the tabletop, meets and climbs the pyramid, and eventually returns to the tabletop. We define the deflection angle $d$ of the geodesic as shown in the diagram.
- the nearer the path goes to the top vertex the greater $d$ is,
- the steeper the pyramid the greater $d$ is,
- there is a complicated dependence on the angle of approach and where the geodesic first hits the pyramid. (These two factors together determine how near the line goes to the top vertex.)
| number of triangles crossed by geodesic |
DEFLECTION equilateral triangles (this is obviously a special case of the more general isosceles case with $z=60^{\circ}$) |
DEFLECTION isosceles triangles |
|
2 Image

|
$30^{\circ}$ | $(2z-90)^{\circ}$ |
|
3 Image
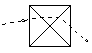
|
$60^{\circ}$ | $(4z-180) ^{\circ}$ |
|
4 Image

|
$90^{\circ}$ | $(6z-270) ^{\circ}$ |
To see how we can prove this, let's look at the situation when the geodesic crosses just two of the isosceles triangles. Remember that when they are flattened the geodesic is just a straight line but, to find the deflection in the plane, we have to put the pyramid up again in its initial position.
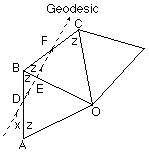
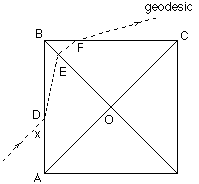
Now stand up the pyramid in its original position.
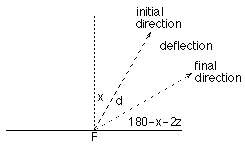
At $F$ we see that $d=90^{\circ}-x-(180^{\circ}-x- 2z)=2z-90^{\circ}$
You can try proving the formulae when the geodesic crosses 3 or 4 triangles.
We see that the more triangles the geodesic crosses the greater $d$ is, and the nearer the line goes to the top vertex, the more triangles it crosses. This is rule (i) above.
Also the greater the value of $z$, the greater $d$ is, and the steeper the pyramid the greater the value of $z$. This is rule (ii) above.
Notice that given that the geodesic crosses a certain number of triangles, the deflection does not depend on $x$. However the number of triangles crossed does depend on $x$ and on the length $A D$. For the equilateral case the conditions, with all the edge lengths of one unit, are:
The geodesic crosses only two triangles if $A D+\frac{\sqrt{3}}{2}\cot x > \frac{3}{2}$.
The geodesic crosses only three triangles if $A D+\frac{\sqrt{3}}{2}\cot x < \frac{3}{2}$ and $A D+\sqrt{3}\cot x> 1$.
The geodesic crosses only four triangles if $A D+\sqrt{3}\cot x< 1$ and $A D+\frac{\sqrt{3}}{2}\cot x> \frac{1}{2}$,
so this is quite complicated.
**
This experiment models the deflection of an object in the gravitational field of another object, e.g. the deflection of a comet in the gravitational field of the sun. The vertex of the pyramid represents the sun, a heavy object producing curvature around it. The geodesic is the path of the comet. If it is far away (so that the geodesic never touches the pyramid) there is no deflection. If it
passes very close to the vertex of the pyramid the deflection is large.
**
3. Final problem
You should have found the following values of $E$:
For any triangulation (regular or irregular) of a sphere, $E=720^{\circ}$.
For any triangulation of a doughnut, $E=0$.
For any triangulation of a doughnut with two holes, $E=-720^{\circ}$.
e.g. For a cube: gap angle at each vertex $=360^{\circ}-(3\times 90^{\circ}) =90^{\circ}$, number of vertices $=8$ so $E=8\times 90^{\circ}=720^{\circ}$.

For a doughnut a simple triangulation looks like the sketch.
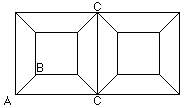
We can stick together two one-holed doughnuts to give a doughnut with two holes, as seen from above in the sketch. There are now 8 type $A$ vertices, 16 type $B$ vertices and 4 type $C$ vertices, where the gap angle is 0.
The theorem is the Gauss- Bonnet theorem which says that the total curvature of a 2-dimensional closed surface depends only on its topology.