Loo Roll Emergency
When the roll of toilet paper is half as wide, what percentage of the paper is left?
Problem
New toilet rolls are cylindrical, 12 cm in diameter, and the cardboard tube in the middle is 4 cm in diameter.
Image
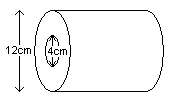
My roll has diameter 6 cm, so it looks about half the size.
What percentage of the toilet paper is left?
Student Solutions
The amount of toilet paper left will be proportional to the area of the paper on the cross-section of the roll. The cross sections of the two rolls are shown below.

On the new roll, this area is $\pi\times6^2-\pi\times2^2=36\pi-4\pi=32\pi$ cm$^2.$
On my roll, this area is $\pi\times3^2-\pi\times2^2=9\pi-4\pi = 5\pi$ cm$^2.$
So $\frac{5}{32}=15.625\%$ of the toilet paper is left.
Image

On the new roll, this area is $\pi\times6^2-\pi\times2^2=36\pi-4\pi=32\pi$ cm$^2.$
On my roll, this area is $\pi\times3^2-\pi\times2^2=9\pi-4\pi = 5\pi$ cm$^2.$
So $\frac{5}{32}=15.625\%$ of the toilet paper is left.
