Inner Rectangle
If the shape on the inside is a rectangle, what can you say about the shape on the outside?
Problem
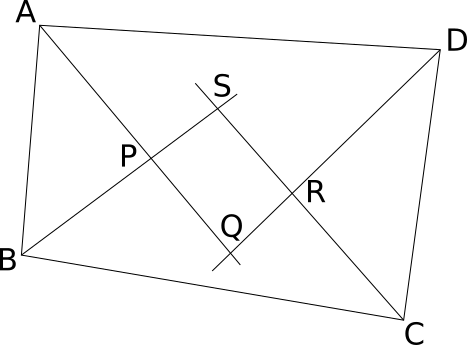
The quadrilateral ABCD has angle bisectors drawn from each of its vertices. These angle bisectors meet to form another quadrilateral PQRS.
If PQRS is a rectangle, what can you say about ABCD?
Image
Student Solutions
If PQRS is a rectangle, then the angle at P is a right angle, and so the opposite angle at P is also a right angle, as shown in the diagram below. Since the lines drawn are angle bisectors, the green angles are equal, the orange angles are equal and the blue angles are equal.
Image

By triangle ABP, the green angle and the orange angle must add up to 90$^\text{o}$.
Similarly, from triangle AQD, which has a right angle at Q, the blue angle and the orange angle must add up to 90$^\text{o}$.
So the green and the blue angles must be the same. Continuing, the angles at A and C must also be equal, so opposite angles of ABCD are equal. Which means that ABCD must be a parallelogram.
