Dividing a Square
A square is divided into three shapes which all have equal areas. Can you find the length of this side?
Problem
Three lines have been drawn from the centre of this square to split it into two congruent trapezia and a pentagon.
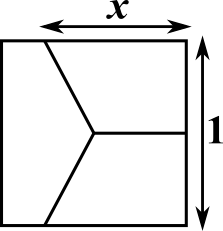
The side length of the square is 1, and the areas of the three shapes are all equal.
What is the length $x$?
This problem is adapted from the World Mathematics Championships
Image

The side length of the square is 1, and the areas of the three shapes are all equal.
What is the length $x$?
This problem is adapted from the World Mathematics Championships
Student Solutions
Splitting the square into rectangles and triangles
Using a vertical line to break each parallelogram into a square and a triangle, and another vertical line to break the pentagon into a rectangle and a triangle, lots of congruent shapes emerge, as shown below.
The areas of the purple squares are $\tfrac{1}{4}$, because the horizontal distance from the centre to the edge of the large square if $\tfrac{1}{2}$ and half of the side length is $\frac{1}{2}$, and $\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$. The four triangles are all congruent and their areas have been labelled $A$.
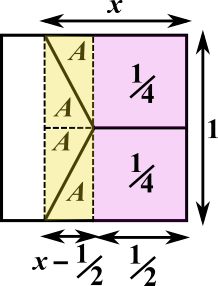
The area of one of the trapezia is $\frac{1}{4}+A$, so $\frac{1}{4}+A=\frac{1}{3}$, so $A=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$
The yellow area is $1\times\left(x-\frac{1}{2}\right)=x-\frac{1}{2}$, so $4A=x-\frac{1}{2}$. $$\begin{align}&4A=\tfrac{4}{12}=\tfrac{1}{3}\\
\Rightarrow&\tfrac{1}{3}=x-\tfrac{1}{2}\\
\Rightarrow&x=\tfrac{1}{3}+\tfrac{1}{2}=\tfrac{5}{6}\end{align}$$
Using the formula for the area of a trapezium
The area of the trapezium coloured yellow in the diagram below is $\frac{1}{2}\times(a+b)\times h=\frac{1}{2}\times\left(x+\frac{1}{2}\right)\times\frac{1}{2}=\frac{1}{4}x+\frac{1}{8}$.

So $\frac{1}{4}x+\frac{1}{8}=\frac{1}{3}$, so $\frac{1}{4}x=\frac{1}{3}-\frac{1}{8}$, so $x=\frac{4}{3}-\frac{1}{2}=\frac{5}{6}$.
Using a vertical line to break each parallelogram into a square and a triangle, and another vertical line to break the pentagon into a rectangle and a triangle, lots of congruent shapes emerge, as shown below.
The areas of the purple squares are $\tfrac{1}{4}$, because the horizontal distance from the centre to the edge of the large square if $\tfrac{1}{2}$ and half of the side length is $\frac{1}{2}$, and $\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$. The four triangles are all congruent and their areas have been labelled $A$.
Image

The area of one of the trapezia is $\frac{1}{4}+A$, so $\frac{1}{4}+A=\frac{1}{3}$, so $A=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$
The yellow area is $1\times\left(x-\frac{1}{2}\right)=x-\frac{1}{2}$, so $4A=x-\frac{1}{2}$. $$\begin{align}&4A=\tfrac{4}{12}=\tfrac{1}{3}\\
\Rightarrow&\tfrac{1}{3}=x-\tfrac{1}{2}\\
\Rightarrow&x=\tfrac{1}{3}+\tfrac{1}{2}=\tfrac{5}{6}\end{align}$$
Using the formula for the area of a trapezium
The area of the trapezium coloured yellow in the diagram below is $\frac{1}{2}\times(a+b)\times h=\frac{1}{2}\times\left(x+\frac{1}{2}\right)\times\frac{1}{2}=\frac{1}{4}x+\frac{1}{8}$.
Image

So $\frac{1}{4}x+\frac{1}{8}=\frac{1}{3}$, so $\frac{1}{4}x=\frac{1}{3}-\frac{1}{8}$, so $x=\frac{4}{3}-\frac{1}{2}=\frac{5}{6}$.
