Clock Angle
What is the angle between the the hands of a clock at 8:24?
Problem
What is the angle between the hands of a clock at 8:24?
This problem is adapted from the World Mathematics Championships
Student Solutions
The diagram below shows the useful parts of the clock face.
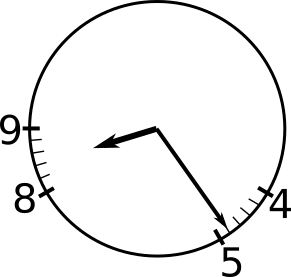
Working in clock minutes
We know that the minute hand has moved through 4 out of the 5 minute markers between the 4 and the 5, but as don't yet know how many of the minute markers between the 8 and the 9 the hour hand has turned through.
The hour hand will turn through 5 minute markers in 1 hour, which is 60 minutes. So it will take 60$\div$5 = 12 minutes to turn through each minute marker.
24 = 2$\times$12, so in the 24 minutes since 8 o'clock, it will have turned through 2 minute markers. This is shown on the diagram below.
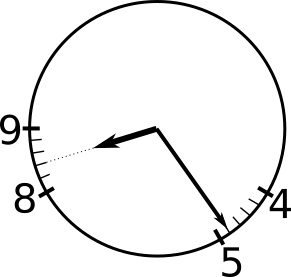
There are 15 minute markers between the 5 and the 8. The minute hand is one minute marker before the 5 and the hour hand is 2 minute markers after the 8, so there are 15 + 1 + 2 = 18 minute markers between the two hands.
There are 60 minute markers on the whole clock, and so 60 minute markers represent 360 degrees. 60$\times$6 = 360, so each minute marker contains 6 degrees.
So the angle between the hands is 18$\times$6$^{\text{o}}$ = 108$^{\text{o}}$.
Working in degrees
There are 60 minute markers on the clock, and so 60 minute markers represent 360 degrees. 60$\times$6 = 360, so each minute marker contains 6 degrees.
The angle between each pair of numbers shown on the clock is 6$\times$5 = 30$^{\text{o}}$, since it takes the minute hand 5 minutes to turn from one number to the next.
These angles are shown on the diagram below, where the angle in each yellow sector is 30$^{\text{o}}$ and the angle in the blue sector is 6$^{\text{o}}$.

The hour hand takes 60 minutes to turn through the yellow sector between the 8 and the 9, which is a turn of 30$^{\text{o}}$. After 24 minutes, it will have turned through $\frac{24}{60}$ of the 30$^{\text{o}}$. $\frac{24}{60}=\frac{12}{30}$ so $\frac{24}{60}$ of 30$^{\text{o}}$ is the same as $\frac{12}{30}$ of 30$^{\text{o}}$, which is 12$^{\text{o}}$.
This angle is shown on the diagram below, where the angle in the red sector is 12$^{\text{o}}$ (and the angles in the yellow and blue sectors are still 30$^{\text{o}}$ and 6$^{\text{o}}$ respectively).
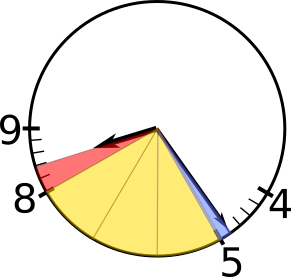
So the angle between the minute hand and the hour hand is 6$^{\text{o}}$ + 3$\times$30$^{\text{o}}$ + 12$^{\text{o}}$, which is 108$^{\text{o}}$.
Image

Working in clock minutes
We know that the minute hand has moved through 4 out of the 5 minute markers between the 4 and the 5, but as don't yet know how many of the minute markers between the 8 and the 9 the hour hand has turned through.
The hour hand will turn through 5 minute markers in 1 hour, which is 60 minutes. So it will take 60$\div$5 = 12 minutes to turn through each minute marker.
24 = 2$\times$12, so in the 24 minutes since 8 o'clock, it will have turned through 2 minute markers. This is shown on the diagram below.
Image

There are 15 minute markers between the 5 and the 8. The minute hand is one minute marker before the 5 and the hour hand is 2 minute markers after the 8, so there are 15 + 1 + 2 = 18 minute markers between the two hands.
There are 60 minute markers on the whole clock, and so 60 minute markers represent 360 degrees. 60$\times$6 = 360, so each minute marker contains 6 degrees.
So the angle between the hands is 18$\times$6$^{\text{o}}$ = 108$^{\text{o}}$.
Working in degrees
There are 60 minute markers on the clock, and so 60 minute markers represent 360 degrees. 60$\times$6 = 360, so each minute marker contains 6 degrees.
The angle between each pair of numbers shown on the clock is 6$\times$5 = 30$^{\text{o}}$, since it takes the minute hand 5 minutes to turn from one number to the next.
These angles are shown on the diagram below, where the angle in each yellow sector is 30$^{\text{o}}$ and the angle in the blue sector is 6$^{\text{o}}$.
Image

The hour hand takes 60 minutes to turn through the yellow sector between the 8 and the 9, which is a turn of 30$^{\text{o}}$. After 24 minutes, it will have turned through $\frac{24}{60}$ of the 30$^{\text{o}}$. $\frac{24}{60}=\frac{12}{30}$ so $\frac{24}{60}$ of 30$^{\text{o}}$ is the same as $\frac{12}{30}$ of 30$^{\text{o}}$, which is 12$^{\text{o}}$.
This angle is shown on the diagram below, where the angle in the red sector is 12$^{\text{o}}$ (and the angles in the yellow and blue sectors are still 30$^{\text{o}}$ and 6$^{\text{o}}$ respectively).
Image

So the angle between the minute hand and the hour hand is 6$^{\text{o}}$ + 3$\times$30$^{\text{o}}$ + 12$^{\text{o}}$, which is 108$^{\text{o}}$.
