Split Clock Face
Use 2 straight lines to split the clock face into 3 parts so that the sums of the numbers in each of the parts are equal.
Problem
Image
Use 2 straight lines to split the clock face into 3 parts, so that the sums of the numbers in each of the parts are equal.
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer:
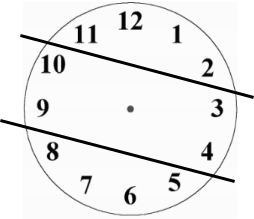
Each sum equal to $\frac{1}{3}$ of $1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12$
$=\frac13$ of $78=26$
2 of the 3 parts will consist only of numbers that are next to each other on the clock face, as shown on the right
Finding numbers that work
12 with 1 or 12 not with 1
12 + 1 = 13 12 + 11 = 22
12 + 1 + 2 = 15 12 + 11 + 10 = 32 too big
11 + 12 + 1 + 2 = 26
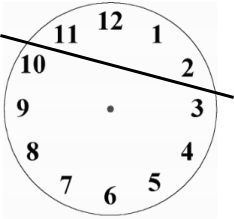
10 + 3 = 13
10 + 3 + 9 = 22
10 + 3 + 9 + 4 = 26

check: 5 + 6 + 7 + 8 = 26 too.
Using algebra
Of the two sections of touching numbers on the clock face that add up to 26, at most one of them will contain the 12 and the 1. So at least one of them will not contain the 12 and the 1, so at least one of them will be a set of ascending numbers (that go up by 1 each time).
If the smallest of the numbers is $n$, then the next one will be $n+1$, the next one will be $n+2$ and so on. So we need either $n+(n+1)=26$, or $n+(n+1)+(n+2)=26$, or $n+(n+1)+(n+2)+(n+3)=26$, and so on.
If $n+(n+1)=26$, then $2n+1=26$, so $2n=25$ so $n=12.5$, which is not a number on the clock face.
If $n+(n+1)+(n+2)=26$, then $3n+3=26$, so $3n=23$ so $n=7.\dot{6}$, which is not a number on the clock face.
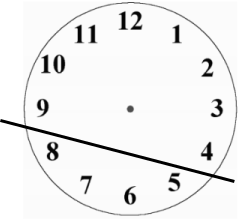
If $n+(n+1)+(n+2)+(n+3)=26$, then $4n+6=26$, so $4n=20$ so $n=5$. So $5 + 6 + 7 + 8 = 26$, and so one of the lines could go here.
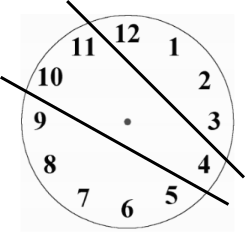
Now choosing where the other line might go, note that $9+10=19<26$ but $9+10+11=30>26$, so 9 and 10 must go with some numbers from the right hand side of the clock face. $9+10+4=23<26$ but $9+10+4+3=26$.
That would leave $11+12+1+2=26$ as well. So the clock face can be split up as shown below.

Note: this method gives us a way to check that there is no other way to do this.
If $n+(n+1)+(n+2)+(n+3)=26$, then $n=5$, and we have one way to split up the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)=26$, then $5n+10=26$, so $5n=16$ so $n=3.2$, which is not a number on the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)+(n+5)=26$, then $6n+15=26$, so $6n=11$ so $n=1.8\dot{3}$, which is not a number on the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)+(n+5)+(n+6)=26$, then $7n+21=26$, so $7n=5$ so $n=\frac{5}{7}<1$. There are no numbers less than 1 on the clock face, so, since adding more numbers will only make $n$ smaller, this will not work for any other sums of consective numbers.
Image

Each sum equal to $\frac{1}{3}$ of $1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12$
Image

2 of the 3 parts will consist only of numbers that are next to each other on the clock face, as shown on the right
Finding numbers that work
12 with 1 or 12 not with 1
12 + 1 = 13 12 + 11 = 22
12 + 1 + 2 = 15 12 + 11 + 10 = 32 too big
11 + 12 + 1 + 2 = 26
Image

10 + 3 = 13
10 + 3 + 9 = 22
10 + 3 + 9 + 4 = 26
Image

Using algebra
Of the two sections of touching numbers on the clock face that add up to 26, at most one of them will contain the 12 and the 1. So at least one of them will not contain the 12 and the 1, so at least one of them will be a set of ascending numbers (that go up by 1 each time).
If the smallest of the numbers is $n$, then the next one will be $n+1$, the next one will be $n+2$ and so on. So we need either $n+(n+1)=26$, or $n+(n+1)+(n+2)=26$, or $n+(n+1)+(n+2)+(n+3)=26$, and so on.
If $n+(n+1)=26$, then $2n+1=26$, so $2n=25$ so $n=12.5$, which is not a number on the clock face.
If $n+(n+1)+(n+2)=26$, then $3n+3=26$, so $3n=23$ so $n=7.\dot{6}$, which is not a number on the clock face.
If $n+(n+1)+(n+2)+(n+3)=26$, then $4n+6=26$, so $4n=20$ so $n=5$. So $5 + 6 + 7 + 8 = 26$, and so one of the lines could go here.
Image

Now choosing where the other line might go, note that $9+10=19<26$ but $9+10+11=30>26$, so 9 and 10 must go with some numbers from the right hand side of the clock face. $9+10+4=23<26$ but $9+10+4+3=26$.
That would leave $11+12+1+2=26$ as well. So the clock face can be split up as shown below.
Image

Note: this method gives us a way to check that there is no other way to do this.
If $n+(n+1)+(n+2)+(n+3)=26$, then $n=5$, and we have one way to split up the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)=26$, then $5n+10=26$, so $5n=16$ so $n=3.2$, which is not a number on the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)+(n+5)=26$, then $6n+15=26$, so $6n=11$ so $n=1.8\dot{3}$, which is not a number on the clock face.
If $n+(n+1)+(n+2)+(n+3)+(n+4)+(n+5)+(n+6)=26$, then $7n+21=26$, so $7n=5$ so $n=\frac{5}{7}<1$. There are no numbers less than 1 on the clock face, so, since adding more numbers will only make $n$ smaller, this will not work for any other sums of consective numbers.
