Black and Gold Storeys
Problem
A building has 50 storeys. 25 of the storeys are painted black and 25 are painted gold.
The sum of the number of gold storeys in the top half and the number of black storeys in the bottom half of the building is 28.
How many gold storeys are there in the top half of the building?
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: 14
Using reasoning
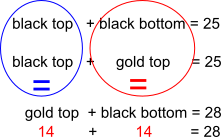
Using a table


$25-a=25-b\therefore a=b$

Using symbols for some of the numbers
Gold storeys in top half: $x$
Black storeys in bottom half: $y$
Given that $x+y = 28$
Gold storeys in the bottom half: $25-x$
Black storey in the bottom half: $y$
$25-x+y=25 \Rightarrow x=y$
So $x+y=28$ means $x$ and $y$ are both $14$, since $x=y$
Using symbols for all of the numbers
$a$ gold storeys in the top half of the building.
$b$ gold storeys in the bottom half of the building.
$c$ black storeys in the top half of the building.
$d$ black storeys in the bottom half of the building.
Then:
$a+b$ = 25 (1)
$c+d$ = 25 (2)
$a+c$ = 25 (3)
$b+d$ = 25 (4)
$a+d$ = 28 (5)
(1) $-$ (4): $a+b-b-d$ = 0 $\Rightarrow a-d$ = 0 $\Rightarrow a$ = $d$
(5) becomes $a+a$ = 28, so $a$ = 14
