Overlapping Beer Mats
Can you find the area of the overlap when these two beer mats are placed on top of each other?
Problem
Two beer mats, each the shape of a regular hexagon with area 36cm$^2$, are placed on top of each other, as shown below.
Image

If they are placed so that the corner of the lower beer mat is in the centre of the higher beer mat, as shown below, what is the area of the overlap?
Image

If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
This problem is adapted from the World Mathematics Championships
Student Solutions
The top beer mat, outlined in red in the diagram below, can be split into triangles from its centre, as shown below.
Image
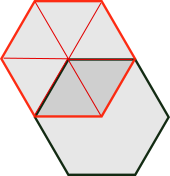
Because the hexagon is regular, the triangles are all the same, so each one will have area 6 cm$^2$ (since the area of the whole beer mat is 36$=$6$\times$6 cm$^2$).
So, since the overlap consists of 2 of the triangles, its area is 12 cm$^2$.
