Lattice Points on a Line
How many lattice points are there in the first quadrant that lie on the line 3x + 4y = 59 ?
Problem
A point whose x and y coordinates are both whole numbers is called a lattice point.
How many lattice points that lie on the line $3x+4y=59$ are there in the first quadrant (where both x and y coordinates are positive)?
This problem is adapted from the World Mathematics Championships
Student Solutions
Using a table of values
Points in the first quadrant have $x,\hspace{2mm}y>0$, so we could begin by substituting values into the equation of the line to check for lattice points on the line.
Using the table below, we can try positive whole numbers for $x$, and then find the value of $3x$. If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point. This is shown on the first line of the table.
If $x=2$, then $3x=6$, so $4y$ must be $53$ since $6+53=59$, so $y=53\div 4=13.25$. So the point $(2,13.25)$ lies on the line, but it is not a lattice point.
Filling in the whole table will give all of the possible lattice points. Remember that $y$ needs to be positive, so $3x$ must not be greater than $59$, so $x$ must be less than $20$ (since $3\times 20=60>59$). So the table only needs to go up to $x=19$.
Counting the points in the table with whole number $y$ coordinates, there are 5 lattice points. Plotting these points gives the graph below (the lattice points are marked in red).
Using gradient triangles
The gradient of the line is $-\frac{3}{4}$. You can work this out by considering changes in $x$ and $y,$ or by rearranging $3x+4y=59$ into $y=-\frac{3x}{4}+\frac{59}{4}$.
This means that every time $x$ increases by $4$, $y$ decreases by $3$. This is shown on the diagram below.
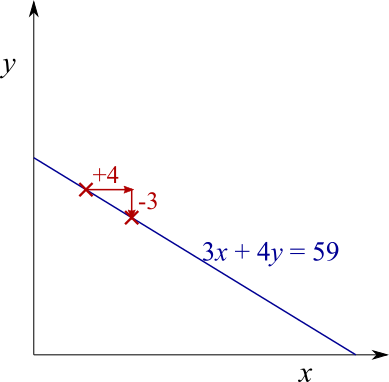
So, if you start at a lattice point, then there will be another lattice point $4$ to the left and $3$ down, and another one $8$ to the left and $6$ down, and so on. There will also be another lattice point $4$ to the right and $3$ up, and so on. So the lattice points, if there are any, will be evenly spaced along the $x$-axis at intervals of $4$, as shown below - where this time, we assume that the dark red crosses mark lattice points.
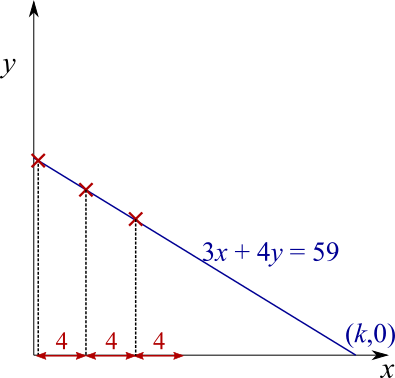
That means that, if we can find a lattice point on the line between $x=0$ and $x=4$, then we can quickly find all of the lattice points by adding $4$ to the $x$ coordinate until we get to $k$ (where $k$ is the $x$-intercept, as shown above).
However, if we can't find a lattice point between $x=0$ and $x=4$, then there won't be any lattice points at all, because lattice points should be at intervals of $4$, so there can't be an interval of $4$ that doesn't contain one.
If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point.
Then there are also lattice points when $x=5, 9, 13, ...$. To work out how many there are in the first quadrant, we need to find the value of $k$, because if $x>k$ then the lattice point will not be in the first quadrant. When $x=k$, $y=0$, and so $3\times k+4\times 0=59$, so $k=59/3=19\frac{2}{3}$.
So the lattice points have $x$-coordinates $1, 5, 9, 13$ and $17$ - which means there are $5$ lattice points.
Using factorisation and properties of numbers
Suppose $(a,b)$ is lattice point on the line $3x+4y=59$ in the first quadrant. Then $a$ and $b$ are positive whole numbers with $3a+4b=59$.
$3a+4b$ can be written as $3(a+b)+b$. This is useful because, starting from $3(a+b)+b=59$, $3(a+b)=59-b$, so $59-b$ must be a multiple of $3$.
Also, since $a$ is positive, $3a$ is also positive, and so $4b<59$, so $b<59\div4$, so $b<14.75$, so $b\le 14$, since $b$ is a whole number.
That means that $59-b\ge 59-14$, so $59-b\ge 45$.
So $59-b$ is a multiple of $3$ that is between $45$ and $59$ ($b>0$ so $59-b<59$). So $59-b$ could be $45, 48, 51, 54$ or $57$. From each of those $5$ options, we can find $b$, and then $a+b$, and then $a$. So there are $5$ lattice points which satisfy the equation - so there are $5$ lattice points on the line.
