Octagonal Ratio
Can you find the ratio of the area shaded in this regular octagon to the unshaded area?
Problem
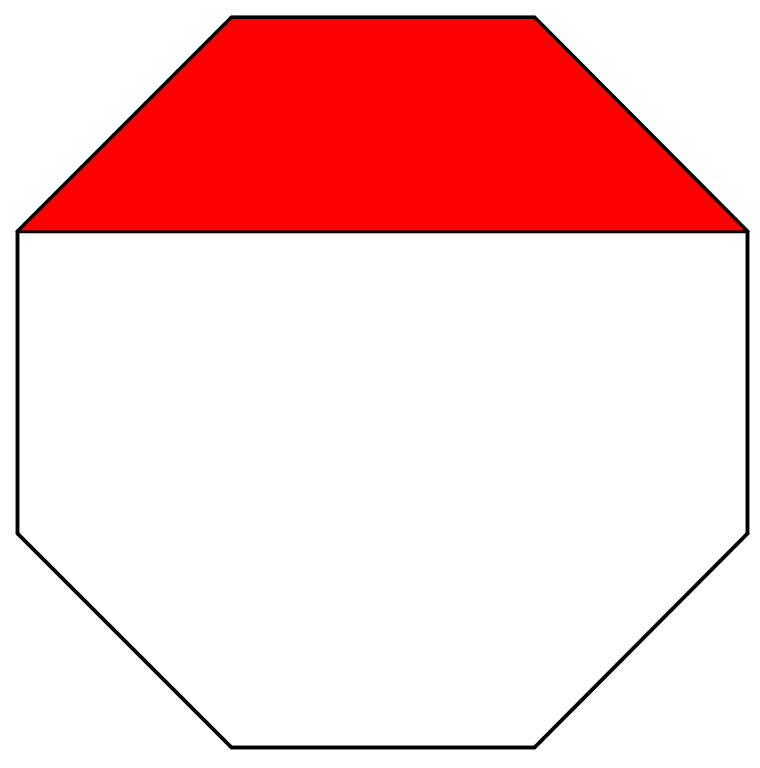
The diagram shows a regular octagon.
What is the ratio of the area of the shaded part of the octagon to the area of the unshaded part of the octagon?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
Dividing the octagon into rectangles and triangles
By drawing some extra lines you get this picture:
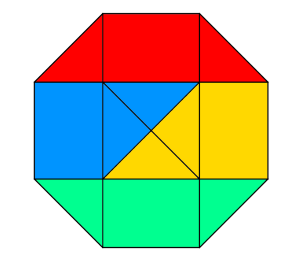
The red and green triangles are right-angled isosceles triangles with a hypotenuse equal to the side length of the octagon.
The blue and yellow triangles are also right-angled isoseles triangles, and as the central square's length is the same as the side lenght of the octagon, these triangles are congruent to the red and green triangles.
There is one rectangle and two triangles shaded in each of the four colours, so the four shaded areas are equal. Therefore the ratio of the shaded to unshaded parts of the original octagon is $1:3$.
Using the centre of the octagon
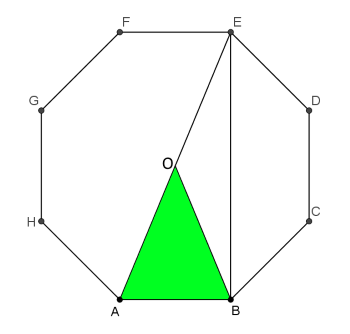
AE divides the octagon in half.
The green triangle is $\frac{1}{8}$ of the total area of the octagon.
Triangle ABE has the same base and twice the height, so twice the area, so is $\frac{1}{4}$ of the total area of the octagon.
So Trapezium BCDE is $\frac{1}{4}$ of the total area.
So the ratio is $1:3$.
Finding areas of shapes
We can label the side length as $1$ since we are looking for ratios between areas, so it doesn't matter how big the octagon is. Three helpful shapes are drawn in. Finding their areas will enable us to find the areas of the shaded and unshaded parts of the octagon.
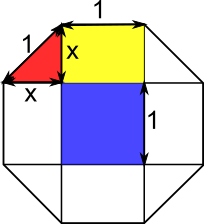

The area of the red triangle is $\frac{1}{2}\times x\times x=\frac{1}{2}x^2.$ Applying Pythagoras' Theorem to the red triangle gives $x^2+x^2=1,$ so $x^2$ must be $\frac{1}{2},$ so $\frac{1}{2}x^2$ must be $\frac{1}{4}.$ So the area of the red triangle is $\frac{1}{4}.$

The area of the yellow rectangle is $1\times x=x.$ Since $x^2=\frac{1}{2},$ $x=\sqrt{\frac{1}{2}}=\frac{1}{\sqrt2}.$ So the area of the yellow rectangle is $\frac{1}{\sqrt2}.$

The area of the blue square is $1$.

So the area of the shaded part of the octagon is $\frac{1}{4}+\frac{1}{\sqrt2}+\frac{1}{4}=\frac{1}{2}+\frac{1}{\sqrt2}$

And the area of the unshaded part of the octagon is $\frac{1}{\sqrt2}+1+\frac{1}{\sqrt2}+\frac{1}{4}+\frac{1}{\sqrt2}+\frac{1}{4}=1\frac{1}{2}+\frac{1}{\sqrt2},$ which is the same as $3\times\left(\frac{1}{2}+\frac{1}{\sqrt2}\right),$ which is $3$ times the shaded area.
So the ratio of the shaded area to the unshaded area is $1:3.$
