Swapping Sweets
If two girls each take a sweet from each other's bags, what is the probability that they end up with what they started with?
Problem
Kate and Anna each have a bag that contains a red sweet, a blue sweet, a green sweet and a yellow sweet.
Without looking, Kate takes a sweet out of her bag and puts it into Anna's bag. Then, without looking, Anna takes a sweet from her bag and puts it into Kate's bag.
What is the probability that after this, each bag contains a red sweet, a blue sweet, a green sweet and a yellow sweet?
This problem is adapted from the World Mathematics Championships
Student Solutions
Using a tree diagram
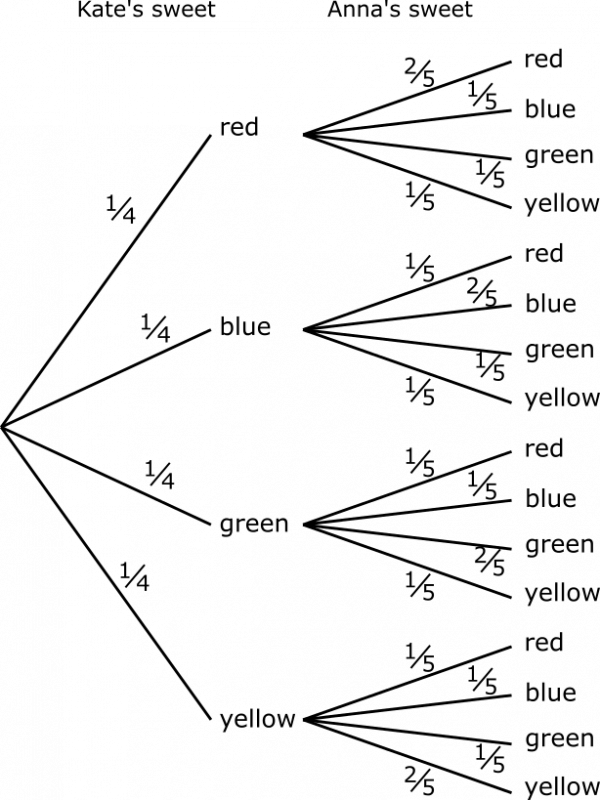
There are two stages here - the sweet that Kate removes, and the sweet that Anna removes - and so a two-stage tree diagram will be helpful.
When Kate takes a sweet out of her bag, there are 4 to choose from, and they are all different colours - so the probability of choosing each colour is $\frac{1}{4}$.
When Anna takes a sweet out of her bag, there are 5 to choose from. If Kate put a red sweet into Anna's bag, then there are two red sweets, so the probability that Anna chooses a red sweet is $\frac{2}{5}$. There is still only one blue sweet, one green sweet and one yellow sweet, so the probability that she chooses each of the other colours is $\frac{1}{5}$. Similarly, if Kate put a blue sweet into Anna's bag, then the probability that Anna chooses a blue sweet is $\frac{2}{5}$, and the probability that she chooses each of the other colours is $\frac{1}{5}$ - and so on.
This is shown on the tree diagram below.
The two bags will each end up with one sweet of each colour if the sweet that Anna puts into Kate's bag is the same colour as the sweet that Kate has put into Anna's bag. Those possibilities are highlighted on the tree diagram below.
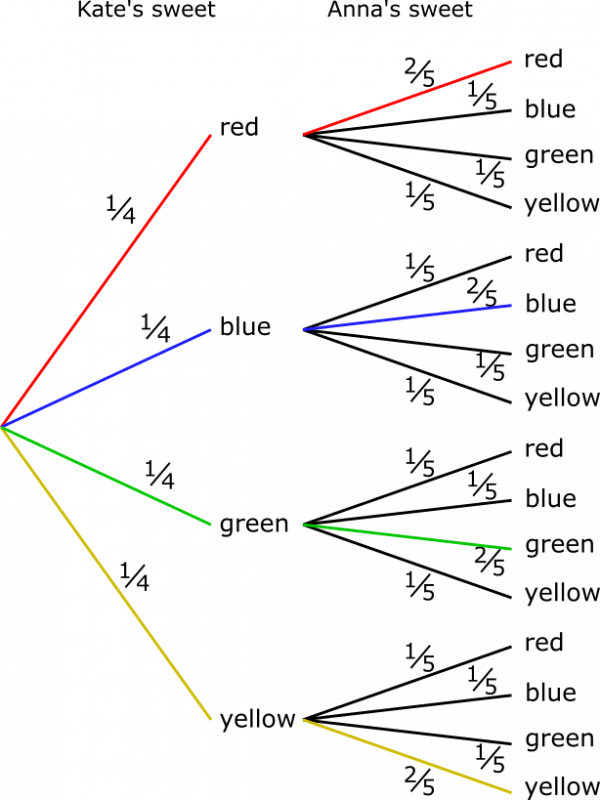
The probability of going along the red path is $\frac{1}{4}\times\frac{2}{5}=\frac{1}{10}$. The probability of going along each of the other paths is also $\frac{1}{10}$, so the probability that both bags end up containing one sweet of each colour will be $\frac{1}{10}+\frac{1}{10}+\frac{1}{10}+\frac{1}{10}=\frac{4}{10}=\frac{2}{5}$ .
Thinking carefully about probability
The two bags will each end up with one sweet of each colour if the sweet that Anna puts into Kate's bag is the same colour as the sweet that Kate has put into Anna's bag.
After Kate has put a sweet into Anna's bag, there will be 5 sweets in Anna's bag. 2 of them will be the same colour - and they are also the same colour as the sweet that Kate has just chosen. So, in order to end up with one sweet of each colour in her bag, Anna needs to remove one of these 2.
Since there are 5 sweets in the bag and 2 to choose from of the required colour, the probability that Anna chooses one of those is $\frac{2}{5}$.
There are two stages here - the sweet that Kate removes, and the sweet that Anna removes - and so a two-stage tree diagram will be helpful.
When Kate takes a sweet out of her bag, there are 4 to choose from, and they are all different colours - so the probability of choosing each colour is $\frac{1}{4}$.
When Anna takes a sweet out of her bag, there are 5 to choose from. If Kate put a red sweet into Anna's bag, then there are two red sweets, so the probability that Anna chooses a red sweet is $\frac{2}{5}$. There is still only one blue sweet, one green sweet and one yellow sweet, so the probability that she chooses each of the other colours is $\frac{1}{5}$. Similarly, if Kate put a blue sweet into Anna's bag, then the probability that Anna chooses a blue sweet is $\frac{2}{5}$, and the probability that she chooses each of the other colours is $\frac{1}{5}$ - and so on.
This is shown on the tree diagram below.
Image

The two bags will each end up with one sweet of each colour if the sweet that Anna puts into Kate's bag is the same colour as the sweet that Kate has put into Anna's bag. Those possibilities are highlighted on the tree diagram below.
Image

The probability of going along the red path is $\frac{1}{4}\times\frac{2}{5}=\frac{1}{10}$. The probability of going along each of the other paths is also $\frac{1}{10}$, so the probability that both bags end up containing one sweet of each colour will be $\frac{1}{10}+\frac{1}{10}+\frac{1}{10}+\frac{1}{10}=\frac{4}{10}=\frac{2}{5}$ .
Thinking carefully about probability
The two bags will each end up with one sweet of each colour if the sweet that Anna puts into Kate's bag is the same colour as the sweet that Kate has put into Anna's bag.
After Kate has put a sweet into Anna's bag, there will be 5 sweets in Anna's bag. 2 of them will be the same colour - and they are also the same colour as the sweet that Kate has just chosen. So, in order to end up with one sweet of each colour in her bag, Anna needs to remove one of these 2.
Since there are 5 sweets in the bag and 2 to choose from of the required colour, the probability that Anna chooses one of those is $\frac{2}{5}$.
