From January 2014 to July 2015, NRICH worked with Haringey Council on a five-term project, funded by the London Schools' Excellence Fund, which aimed to raise pupil attainment by improving primary teachers' Maths subject knowledge and pedagogic knowledge. You can read more about the project here.
On 13 October 2015, we held a conference entitled 'Mastering mathematics and the new primary curriculum', which celebrated the achievements of the project and looked forward to further NRICH work in Haringey. The conference comprised two keynote speakers, Professor Mike Askew and Lynne McClure, along with three workshops, two of which were led by Haringey teachers and the third by Michael Hall and Liz Woodham. What follows is a summary of the day.
Introduction
Mike and Lynne spoke for a few minutes about their reasons for 'buying into' mastery. Mike commented that, for him, it was a social justice issue. He thought that the discourse is shifting from 'able children' to 'enabling children'. Lynne explained that teacher expectation (linked to teacher behaviour) has a disproportionately significant effect on children's success and she felt that the principles of mastery will encourage teachers to think differently about expectation.
Keynote 1: Mike
2015-10-13AskewKeynoteFinal.pptx
Bloom was the first to coin the phrase of 'mastery' in the 1960s but it fell out of favour because many felt that children who picked up mathematics quickly were not being challenged.
Mike set us off on a task called Diffy. He challenged us to draw a square and place a number at each corner. At the midpoint of each side, he asked us to write the difference between the numbers at each end and join these new numbers to create a second square and so on. For example, here is my square after doing this three times with my starting numbers 42, 7, 67 and 21:
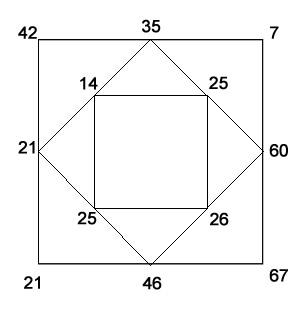
Mike asked us to consider what happens if you continue doing this. This led to a number of follow-up questions:
- Can you keep it going as long as possible?
- What happens if you change the shape e.g. triangles or pentagons?
- What happens if you use fractions?
- What hapens if you do this on a number line?
- What happens if you start with four zeros and expand outwards?
Mike explained that this task illustrates 'depth'. At an elementary level, children are finding differences, but they are also prompted to ask their own questions, perhaps to use algebra. In other words, everyone can work at their own level but it is still possible to have conversations together about the task, which creates a community of mathematicians. Mike suggested that by starting with a problem, the community works through it and you can tap into children's natural problem-solving abilities.
Mike invited us to consider whether learning is based in intelligence or experiences. There is research which says that we are born with a certain amount of aptitude for learning mathematics but this is completely over-ridden by our early years experiences (ref. Robert Plowman?). So, as teachers we should try to provide as rich an environment as possible. Mike urged us to get rid of the 'container' view of potential - most people can learn most things at most ages. Experiences shape what we learn, as suggested by Jo Boaler in her research about the plasticity of the brain.
This challenges the way we group children in the classroom. Do we change the curriculum content to meet individual needs ('ability group') or do we keep the curriculum constant and make it accessible for all (the mastery approach)?
There were a few questions from delegates:
We can't.
2. How will this work in tests?
The pass rate will need to be 90%.
3. How can I fit in intervention groups?
Research by Peter Sullivan in Australia suggests that pre-teaching is the key i.e. identifying four or five children who you think may have difficulty with a topic/concept and giving them a 'foot up' into the lesson beforehand. However, there is a resourcing issue. (Lynne suggested that we need to give very young children experience of a mastery curriculum when they first start school.)
4. Isn't there an issue with the confidence of the teaching force?
Yes, we need to shift from 'teaching about long multiplication' to 'thinking multiplicably'.
Mike went on to explain that Bloom's mastery had three components:
- Giving regular feedback to children in terms of what an individual needs to do to do better;
- Giving children a range of experiences i.e. the same idea in many different ways;
- Depth.
In the time of the National Numeracy Strategy, there was a stepwise view of learning, but by taking longer to make sure that the early concepts are secure, as advocated by the mastery approach, the rate of learning increases rapidly (see image on ppt slide).
Mike explained that poblem solving is central to a mastery approach. Children are offered a problem to start with, then the class explores different solutions in depth. For example, Mike observed a lesson where the task was 24+9. The teacher carefully selected three different solutions to share with everyone (partioning 24 into 23 and 1 to give 23+10; partitioning 24 into 20 and 4 to give 20+13; partitioning 9 into 3 and 6 to give 30+3). Then the class worked on further examples of adding 9 to any two-digit number, selecting one of the three methods each time. This is an example of 'variation'. It is known from research that if we are only shown one example, we think less deeply compared with being given three examples. Chinese classrooms often use this 'one problem, three solutions' approach. The teacher knows which methods to look out for, but this puts the thinking back on the children.
Mike emphasised the shift from 'products' to 'processes' (or, put another way, from 'mathematics' to 'mathematising' where problem solving is central) in a mastery curriculum. Mike share the following sequence of questions:
I have 9 litres of jam. If I have 3l jars, how many jars will I fill?
I have 9 litres of jam. If I have 1l jars, how many jars will I fill?
I have 9 litres of jam. If I have $\frac{1}{2}$l jars, how many jars will I fill?
I have 9 litres of jam. If I have $\frac{1}{3}$l jars, how many jars will I fill?
We were asked to jot down the answers first. Then we were asked to write down the calculation which applied to each one.
The above sequence is an example of variation - the questions are carefully chosen to provide variation through what is kept constant and what is changing. The relationship between the examples is more important than the examples on their own. The questions encourage children to ask themselves "what is the same here and what is different?".
Workshop 2: David Joyce from North Harringay Primary
Mastery for lower-attaining learners and Parents
David is the maths subject leader at North Harringay Primary School. His workshop was in two parts. The first focused on how NRICH tasks engaged low-attaining chlidren in his school and the difference these tasks made to their attainment (see this pdf of PowerPoint slides). The second part described work that David has done with parents of KS1 children at the school. He organised a maths day for them, which gave them an opportunity to try some of the tasks their children had tackled, and to discuss the value of rich tasks in the mathematics classroom generally (see this pdf of PowerPoint slides).
Workshop 3: Michael Hall and Liz Woodham
The role of mastery in developing young mathematicians
20151013HaringeyWorkshop3.pdf
In this workshop, we began by having a go at Round the Two Dice. We discussed the mathematics we used to tackle the task and the 'value added' of this task compared with a worksheet of rounding questions, for example.
Liz introduced the rope image of the five elements for nurturing young mathematicians from Adding it up: Helping children learn mathematics (2001). (The full reference is on the presentation linked above.) We discussed each briefly and Liz suggested that the diagram conveys two messages:
- the rope strands are all the same thickness and length, implying that each strand is of equal importance;
- the strands are interwoven, implying that the five elements complement each other and 'work together'.
Liz explained that, in NRICH's view, the current view of mastery seems to focus on 'conceptual understanding' and 'procedurual fluency' but does not consider the other three elements sufficiently and perhaps in particular does not address 'productive disposition'.
To help teachers to encourage a productive disposition towards mathematics, Liz drew attention to the 'Developing Habits of Mind' page in development on NRICH, which pulls together tasks in four categories:
- Being curious
- Being thoughtful
- Being collaborative
- Being determined.
We discussed which of the five strands Round the Two Dice might help to develop.
Keynote 2: Lynne
Productive disposition and its centrality to the mastery curriculum
LynneMcClurePresentation.pdf
Lynne warmed us up with the 'orchestra' activity in which she assigned us to one of three groups - the first counted in 1s, the second in 10s and the third in 100s. We counted outloud and Lynne 'conducted' so that each group knew when to take over the counting. We tried counting in 1s, 5s and 10s, and discussed how that was different. What if the counting started at 0 or 2 or 4? What would happen if we did 1s and 2s, or 2s and 5s? We were challenged to come up with another pairing which would produce a similar effect. We discussed the possible learning objectives for this activity - fluency in multiples/counting in multiples. We noted that it was about being fluent in number facts, but more than that as it was about appreciation of number too. Perhaps it provoked different mental images and perhaps some of us were aware of auditory patterns?
Lynne referred to the images on slides 3, 4 and 5 of her presentation linked above. She explained that mathematics education is a bit like a seesaw, with computation, memory and 'back to basics' on one side and structure, reasoning and problem solving on the other. She believes that this curriculum acknowledges both sides are important, but that a productive disposition is needed in order for children to flourish.
Lynne gave each table a set of nine cards (see slide 9) and asked them to arrange them so that the ones they most strongly agreed with were at the top. Groups could add an extra if they wished. We walked round to see what other groups had done and talked about the fact that the point of this task is the discussion you have with colleagues as you make decisions.
Lynne talked about the rope image of the five elements for creating young mathematicians (see slide 10 in her presentation and the presentation from Workshop 3 for the full reference) and we discussed what was meant by 'productive disposition'. She pulled out three elements (see slides 13, 14 and 15):
- seeing the value of maths;
- knowing that effort is worth it i.e. that if you work hard, you will be able to do it;
- having a belief that you can do it.
We examined each of these elements in turn:
Value
Lynne posed the following questions:
- What does it mean to value mathematics?
- Does all maths have to be useful?
- What elements of classroom climate woud encourage a view of maths as valuable?
Delegates made the following comments:
- We need to make maths explicit when it comes up in other subjects.
- There should be tangible items in the classroom where children might use their mathematics.
- Teachers need to show their own enthusiasm for maths (or act as if they are enthusiastic!).
- All maths doesn't have to be useful but it is more about the wonder, joy, patterns and creativity.
- What is the definition of 'useful'?
- Children need to be comfortable talking about mistakes and valuing the learning journey, rather than just answers.
- Competitions can be helpful.
Lynne commented that we would like children to understand the structure of mathematics so that they do not think it is all magic. The authority lies with the mathematics, not the teacher.
Belief
Lynne challenged us with the following:
Comments included:
- What about those who believe they can't?
- Mike mentioned that risk-taking is one of five traits that are 'hard-wired' into us (although it's not fixed).
- It's the difference between trying to solve a difficulty yourself and looking for outside help.
- It is important to say that you can nurture change.
Lynne commented that children who are successful are often resilient and expect to be able to do it.
Effort
Lynne asked:
Suggestions included:
- Incude variety.
- Give appropriate feedback i.e. there is always room for improvement, asking what if ...
- Raise aspirations.
- Low threshold high ceiling tasks give immediate success.
- Look for opportunities to take maths out of the classroom where it might be more powerful and memorable.
- Realise the creative aspect of maths (Lynne told us about interviews which she carried out with lots of primary children who, when asked about what they did in maths, listed topics such as calculating, finding percentages etc rather than talking about anything personal that they had created.)
- Use games.
Lynne commented that intrinsic motivation is the most durable (see Carol Dweck's research).
