Counting Counters
Take a counter and surround it by a ring of other counters that
MUST touch two others. How many are needed?
Problem
Image
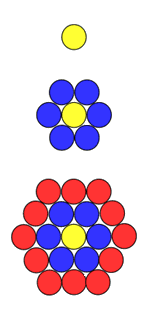
Take a counter and surround it by a ring of other counters that MUST touch two others. How many counters do you need to do this?
Imagine surrounding this ring with more counters.
How many more counters are needed now?
How many counters will there be altogether?
Were you right?
What about a bigger ring? And another? And another?
How many counters will there be in the $9$th ring?
How many do you think there will be in the $100$th ring?
How would you predict how many counters there will be in any ring?
Student Solutions
Jade from Coombe Girls School and Rohaan from North Cross Intermediate correctly spotted the pattern in the number of counters in each ring:
Every ring you add, you are just adding $6$ more counters than the previous ring.
Circle number excluding the counter in the middle $\times6 = $number of counters in that particular layer
Volkan and other pupils at FMV Ozel Erenkoy Isik Primary solved the second part of the problem:
At the end of the third layer, there are; $1+6+12=19$ counters.
At the end of the fourth layer, there are; $19+(3\times6)=37$ counters.
At the end of the seventh layer, there are; $37+(15\times6)=127$ counters.
At the end of the ninth layer, there are; $127+(15\times6)=217$ counters.
Some people solved this part by numbering the counters, starting from one in the middle and counting outwards. Thank you for sending in your solutions!
Teachers' Resources
Why do this problem?
This problem gives an opportunity for children to generalise from a practical situation. It is easy to replicate these patterns in the classroom with counters, bottle tops etc.Possible approach
You could begin by displaying the image in the problem and invite children to talk to a partner about what they notice.After a short time, bring everyone together and ask pairs to share their thoughts. Use their observations to clarify how the images have been created and then lead into the first question. Ensure learners have access to counters and other similar resources to use in order to tackle the task, should they wish.
This task could extend over a few lessons and might culminate in pairs or small groups presenting findings to the rest of the class.
Key questions
Can you describe the pattern?
How many counters will you need to make the next 'one'?
How many counters have you used already?
Can you predict the number of counters you'll need for the next 'one'?
Can you predict the number of counters you'd need for any 'layer'?
