Paired Parabolas
Some parabolas are related to others. How are their equations and graphs connected?
Problem

This resource is from Underground Mathematics.
What's the same and what's different about the following pairs of equations?
- $y=x^2-4$ and $y+x^2-4=0$
- $y=4-9x^2$ and $y+4=9x^2$
- $2y=4x^2-6$ and $-(y-3)=2x^2$
If you were given the following picture, could you suggest the equation of its pair?
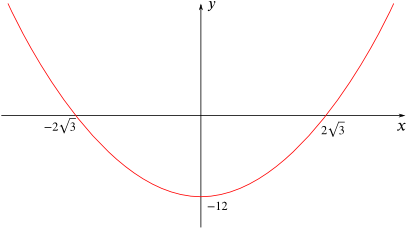
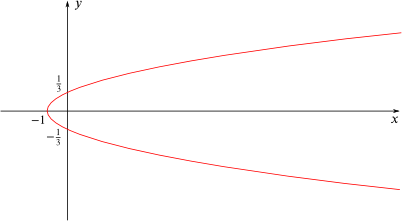
How about if you were given this picture instead?
Could you give the equation of its pair?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Thank you to Minhaj from St Ivo School for his well explained solution to this problem which is given below.
What's the same and what's different about the following pairs of equations?
After rearranging to make $y$ the subject in each equation, it can be seen that for all the parabola pairs, the equations are reflections of each other with the line of reflection being the $x$ axis. So if we defined the first parabola of any of the pairs as $f(x)$, the second parabola would be $-f(x)$.
The obvious features of the equations are that they are all quadratic equations, and they all also revolve around the difference of two squares- in other words for $y= a x^2+b x+c$, $b x=0$. So for example, number 1, $y=x^2-4$, can be written as $y=(x+2)(x-2)$ and $y=4-x^2$ can be written as $y=-(x+2)(x-2)$.
The equation of the pair of the first parabola:
First I will find the equation of this red parabola. It can be seen that this is also an example of difference of two squares so the equation would be $y= x^2-12$ coming from $y=(x+2\sqrt{3})(x-2\sqrt{3})$. So I would guess that the "pair" of this quadratic would have an equation which would show the reflection of this parabola through the $x$ axis: $y=-(x^2-12)$ so $y=12-x^2$ is the equation of the pair.
The equation of the pair of the second parabola:
First of all, this isn't the conventional quadratic with $y=...$. But it is $x=...$ (sideways parabola?). The roots of this graph on the $y$ axis are $\frac{1}{3}$ and $\frac{-1}{3}$ so again it is related to the difference of two squares: $x=(y+\frac{1}{3})(y-\frac{1}{3})$- however this isn't quite the correct equation of this parabola as the graph crosses the $x$ axis when $x=-1$ and not when $x= -\frac{1}{9}$. This means there is a scale factor involved and to find this we do $(-1)/(\frac{-1}{9})=9$. So the actual equation is $x=9(y+\frac{1}{3})(y-\frac{1}{3})= 9y^2-1$. This means the equation of the pair of this graph is $x=1-9y^2$.
