Cubist cuts
Problem
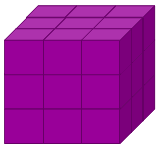
A $3 \times 3 \times 3$ cube may be reduced to unit cubes ($1 \times1 \times1$ cubes) in six saw cuts if you go straight at it.
If after every cut you can rearrange the pieces before cutting straight through, can you do it in fewer? Answer the same question with a $4 \times 4 \times 4$ cube:
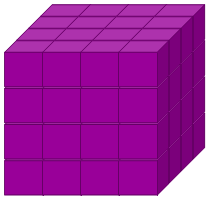
What about a cube of any size (an $n \times n \times n$ cube)?
This problem has been adapted from the book "Sums for Smart Kids" by Laurie Buxton, published by BEAM Education. This book is out of print but can still be found on Amazon.
Getting Started
Use cubes made from smaller cubes (e.g. multilink) to help you. For the 3x3x3 cube, think about "freeing" the centre unit cube.
Student Solutions
Jake, Ryo and Charlie from Moorfield Junior School have explained how to cut up a 3x3x3 cube using 6 cuts:
"We got a 3 by 3 cube and then we cut it 2 times to make 3 lots of 9 cubes. Then we piled all the cubes on top of each other. Then we took another 2 cuts to leave 9 towers of 3 cubes. Next we layed them next to each other. After that we took another 2 cuts to leave the 27 unit cubes."
Chris B, Elliot and Joseph, also from Moorfield Juniors, sent us a diagram to show where these cuts should be:
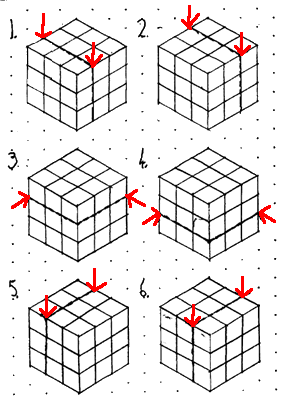
Juliette noticed that it wouldn't be
possible with fewer than 6 cuts:
"We need at least 6 cuts because we need one cut for each face of
the small cube in the middle of the $3\times 3 \times 3$
cube."
Anthony noticed that, with a $4 \times 4
\times 4$ cube, we can use 6 cuts if we rearrange the
cubes:
"First cut the cube in half down the middle, then stack the halves
on top of each other (in an $8 \times 2 \times 4$ arrangement) and
cut down the middle, to make four $4 \times 4$ slices each 1 unit
thick. Then rearrange the cubes into the original arrangement and
repeat the process in the other two directions. This will cut the
cube into $1 \times 1 \times 1$ cubes. It cannot be done with fewer
than 6 cuts because the cubes in the middle will each need at least
one cut for each face"
The $n \times n \times n$ cube is a bit
trickier. Try a few yourself before looking at this
explanation.
First of all let's see how many cuts are
needed to cut the cube into slices 1 unit deep. We can then do this
in each of the three directions to cut the $n \times n \times n$
cube into unit cubes, and can multiply by three to find out how
many cuts are needed in total.
For a cube with side length 3 or 4 units,
we need 2 cuts, as Juliette and Anthony explained. For 5 units,
we'll need an extra cut in each direction. To cut as efficiently as
possible, we should use a method similar to Anthony's: first cut in
half (or as close to in half as possible), then stack up the
"halves" and repeat until we are left with "slices" 1 unit thick.
We can then put the cube back together and repeat for the other two
directions.
The general pattern is: for each doubling
of $n$, we need an extra 3 cuts to cut an $n \times n \times n$
cube into $1 \times 1 \times 1$ cubes. This is shown in the table
below.
| $n$ | Number of cuts |
| $1$ to $2$ | $1 \times3$ |
| $3$ to $4$ | $2 \times3$ |
| $5$ to $8$ | $3 \times3$ |
| $9$ to $16$ | $4 \times3$ |
| $(2^{k-1} + 1)$ to $2^k$ | $k \times3$ |
