Equation or Identity (2)
Problem
Throughout, $A$, $B$ and $C$ are the angles of a triangle.
For each of the following, decide whether it is an identity (true for all triangles) or an equation (there is a triangle for which it is not true).
If it is an identity, true for all triangles, then you should prove it (using trigonometric identities that you already know).
If it is an equation, then give an example of a triangle for which it is not true. You could also try to solve the equation (that is, find all triangles for which it is true).
1. $\sin(A + 2B) = \sin A + 2\sin B \cos(A + B)$.
2. $\tan(A - B) + \tan(B - C) + \tan(C - A) = 0$.
3. $2\sin A \cos^2\left(\frac{B}{2}\right) + 2\cos^2\left(\frac{A}{2}\right)\sin B = \sin(A + B) + \sin(B + C) + \sin(C + A)$.
4. $\sin(A+B) = \cos C$.
5. $\cos C = -\cos(A+B)$.
6. $4(\cos^2 A \cos^2 B + \sin^2 A \sin^2 B) - 2 \sin(2A) \sin(2B) = 3$.
7. $\sin(2A) + \sin(2B) + \sin(2C) = 4\sin A \sin B \sin C$.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
We received lots of solutions to this problem. Thank you to Meghna, Adithya, Agathiyan and Amrit from Hymers College, Ai, Kianoush, Kingsley, Minh, John, Fatemeh, Ali, Alireza, Bow and Disha from Bellerbys College Cambridge and Thomas from BHASVIC Sixth Form College for sending us your solutions. Lots of different techniques were used, so we shall through them one problem at a time.
Meghna, Ai, Kianoush and Kingsley sent us solutions to the first problem. Here is Meghna's solution:
1) $\sin(A + 2B) = \sin A + 2\sin B \cos(A + B)$
IDENTITY
$\begin{align}
\sin{(A+2B)} &= \sin{A}\cos{2B} + \cos{A}\sin{2B}\\
&= \sin{A} (1-2\sin^2{B}) + \cos{A}(2\sin{B}\cos{B})\\
&= \sin{A} -2\sin{A}\sin^2{B} + 2\sin{B}\cos{B}\cos{A}\\
&=\sin{A} + 2\sin{B}(\cos{B}\cos{A} - \sin{B}\sin{A})\\
&=\sin{A} +2\sin{B}\cos{(A + B)}
\end{align}$
Meghna showed that the second problem was an equation:
2) $\tan(A - B) + \tan(B - C) + \tan(C - A) = 0$
EQUATION
Not true when $A=60^\circ$, $B=30^\circ$, $C=90^\circ$
$\tan{(60 - 30)} + \tan{(30 - 90)} + \tan{(90 - 60)} = \frac{\sqrt{3}}{3}$
Agathiyan, Ai and Thomas sent us solutions to problem 3. Thomas showed this was an identity by starting with the left-hand side:
3) $2 \sin{A} \cos^2 {\frac{B}{2}} + 2\cos^2{\frac{A}{2}} \sin{B} = \sin{(A+B)} + \sin{(A+C)} + \sin{(B+C)}$
IDENTITY
Using the double angle identity $\cos(2x)+1 \equiv 2\cos^2x$, we get that
$$\begin{align}
2\sin{A}\cos^2{\frac{B}{2}}+2\cos^2 \frac{A}{2} \sin B & \equiv \sin A (\cos B +1) + \sin B (\cos A +1) \\
&\equiv \sin A \cos B + \sin B \cos A +\sin A +\sin B
\end{align}$$
Then use the angle sum identity $\sin A+B \equiv \sin A \cos B + \sin B \cos A$:
$$\qquad\qquad\qquad\qquad\qquad \equiv \sin(180-C) +\sin A +\sin B$$
We also know that $A+B+C=180^\circ$, so $A=180^\circ-(B+C)$ and likewise for $B$:
$$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \equiv \sin(A+B)+\sin(180-(B+C))+\sin(180-(A+C))$$
Now we notice that $\sin(180-x)=\sin(x)$ for all $x$
$$\qquad\qquad\qquad\qquad\qquad\qquad\quad \equiv \sin(A+B)+\sin(A+C)+\sin(B+C)$$
as required.
Ai also proved this was an identity, but she started by working with the right-hand side:
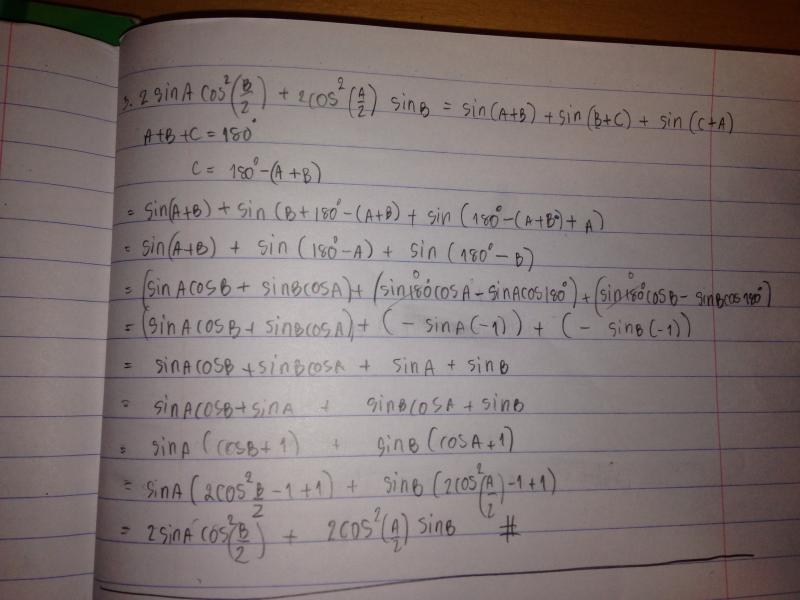
Meghna, Minh, John and Fatemeh sent us solutions to problem 4. Here is Minh, John and Fatemeh's solution:
4) $\sin(A+B) = \cos C$
EQUATION
Since the angles are in a triangle, we have that $A+B+C=180^\circ$ so let us use $A+B=180^\circ -C$:
$$\begin{align}
\sin(A+B) &= \cos C \\
\sin(180^\circ - C) &= \cos C \\
\sin 180^\circ \cos C - \cos 180^\circ \sin C &= \cos C\\
0 - (-1)\sin C &= \cos C\\
\sin C &= \cos C \\
\tan C &= 1 \\
C &= 45^\circ
\end{align}$$So this equation is true provided that $C=45^\circ$. This means that $A$ and $B$ can take any value, provided that $A+B=135^\circ$.
Meghna, Minh, John and Fatemeh sent us solutions to problem 5. Here is Meghna's solution:
5) $\cos{C} = -\cos{(A + B)}$
IDENTITY
$\begin{align}
\cos{C} &= \cos{(180 - (A +B))}\\
&=\cos{180}\cos{(A + B)} + \sin{180}\sin{(A + B)}\\
&= (-1)\cos{(A + B)} + 0\\
&= -\cos{(A + B)}\\
\end{align}$
Meghna sent us the following solution to problem 6:
6) $4(\cos^2{A}\cos^2{B} + \sin^2{A}\sin^2{B}) - 2\sin{2A}\sin{2B} = 3$
EQUATION
Not true when $A=60^\circ, B=30^\circ, C=90^\circ$
$4(\cos^2{60}\cos^2{30} + \sin^2{60}\sin^2{30}) - 2\sin{120}\sin{60} = 4(\frac{6}{16})
- (\frac{3}{2}) = 0$
Adithya, Thomas, Minh, John and Fatemeh sent us solutions to problem 7. Here is Minh, John and Fatemeh's solution:
7) $\sin(2A)+\sin(2B)+\sin(2C)=4\sin A \sin B \sin C$
IDENTITY
Starting with the left hand side:
$$\begin{align}
\sin 2A + \sin 2B +\sin 2C &\equiv \sin 2A + \sin 2B + \sin (360^\circ - 2(A+B)) \\
&\equiv \sin 2A + \sin 2B + \sin 360^\circ \cos(-2(A+B)) \\
&\ + \cos360^\circ \sin (-2(A+B)) \\
&\equiv \sin 2A + \sin 2B + 0 \times \cos(-2(A+B))+ 1\times \sin (-2(A+B)) \\
&\equiv \sin 2A + \sin 2B + \sin (-2(A+B)) \\
&\equiv \sin 2A + \sin 2B - \sin (2(A+B)) \\
&\equiv \sin 2A + \sin 2B - (\sin 2A \cos 2B + \sin 2B \cos 2A) \\
&\equiv \sin 2A (1-\cos2B) + \sin 2B (1-\cos2A) \\
&\equiv \sin 2A (\cos^2 B+\sin^2 B - \cos^2 B + \sin^2 B) \\
&\ + \sin 2B (\cos^2 A+\sin^2 A - \cos^2 A + \sin^2 A) \\
&\equiv \sin 2A (2\sin^2 B) + \sin 2B (2\sin^2 A) \\
&\equiv 2 \sin 2A \sin^2 B + 2 \sin 2B \sin^2 A
\end{align}$$Then looking at the right-hand side:
$$\begin{align}
4\sin A \sin B \sin C &\equiv 4\sin A \sin B \sin (180^\circ -(A+B)) \\
&\equiv 4\sin A \sin B (\sin 360^\circ \cos(-(A+B)) + \cos180^\circ \sin (-(A+B))) \\
&\equiv 4\sin A \sin B (0 \times \cos(-(A+B)) + (-1)\times \sin (-(A+B))) \\
&\equiv 4\sin A \sin B \sin (A+B) \\
&\equiv 4\sin A \sin B (\sin A \cos B + \sin B \cos A) \\
&\equiv 4\sin^2 A \sin B \cos B + 4\sin A \cos A \sin^2 B \\
&\equiv 4\sin^2 A \frac{1}{2}\sin 2B + 4 \left( \frac{1}{2} \sin 2A \right) \sin^2 B \\
&\equiv 2\sin^2 A \sin 2B + 2\sin 2A \sin^2 B \\
&\equiv 2\sin 2A \sin^2 B + 2\sin 2B \sin^2 A
\end{align}$$So the left-hand side is identical to the right-hand side, so we have an identity.
Thomas used a different method to solve this problem. Here is his solution:
The first two terms of the LHS are $\sin(2A)+\sin(2B)$ which is the sum of sines, so we can use the formula
$$\sin x +\sin y =2\sin(\frac{x+y}{2})\cos(\frac{x-y}{2})$$
and the double angle formula, $\sin(2x) \equiv 2\sin x \cos x$, on the final term to give
$$\sin(2A)+\sin(2B)+\sin(2C) \equiv2\sin(A+B)\cos(A-B)+2\sin C \cos C$$
We know that $A+B+C=180^\circ$, so $A+B=180^\circ-C$
$$\qquad\qquad\qquad\qquad\qquad\qquad\quad \equiv2\sin(180-C)\cos(A-B)+2\sin C \cos C$$
and we also know that $\sin(180-x)=\sin(x)$, so we have
$$\qquad\qquad\qquad\quad \equiv 2\sin C(\cos(A-B)+\cos C)$$
Then we can further simplify the RHS by using the sum of cosines formula, that $A+B+C=180^\circ$ and that $\cos (-x)=\cos x$
$$\begin{align}
\cos(A-B)+\cos C &\equiv (2\cos(\frac{A-B+C}{2}) \cos(\frac{A-B-C}{2}) \\
&\equiv 2\cos(\frac{A+C-B}{2}) \cos(\frac{A-(B+C)}{2}) \\
&\equiv 2\cos(\frac{180-B-B}{2}) \cos(\frac{A-(180-A)}{2}) \\
&\equiv 2\cos(\frac{180-2B}{2}) \cos(\frac{2A-180}{2}) \\
&\equiv 2\cos(90-B) \cos(A-90) \\
&\equiv 2\cos(90-B) \cos(90-A)
\end{align}$$
Finally we have that $\cos(90-x)=\sin(x)$, so we have proved the identity since we now have:
$$\begin{align}
\sin(2A)+\sin(2B)+\sin(2C) &\equiv 2\sin(C) \times 2\sin(B)\sin(A) \\
&\equiv 4\sin(A)\sin(B)\sin(C)
\end{align}$$
So we know which problems are equations and which are identities. We also know for which values problem 4 is true. Can you find the values for which problems 2 and 6 are true?

