An Equilateral Triangular Problem
Take an equilateral triangle and cut it into smaller pieces. What can you do with them?
Problem
An Equilateral Triangular Problem printable sheet
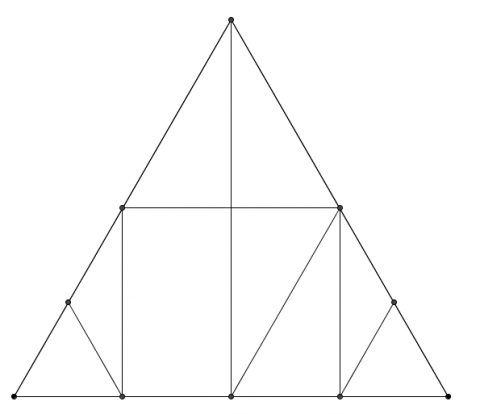
The picture above shows an equilateral triangle, with lines drawn between various midpoints.
Have a go at printing out this triangle, and cutting along the lines to make nine smaller shapes.
What are the angles in each of your smaller shapes?
If the area of the smallest equilateral triangle is one unit, what is the area of each of the other shapes?
We can take a collection of the smaller cut out areas and rearrange them to make different shapes.
Using the nine smaller shapes:
- How many different trapezia (which are not parallelograms) can you make?
- How many different parallelograms (which are not rectangles) can you make?
- How many different rectangles can you make?
- Which other quadrilaterals can you make?
You may find it useful to print out the figure.
Getting Started
What angles/areas do you know?
How can you use the angles/areas you know to work out other angles/areas?
What properties does a trapezium/parallelogram/rectangle have?
Student Solutions
Mahdi from Mahatma Gandhi International School in India, Alyssa from NGHS in the UK and Julia from Tanglin Trust School in Singapore found all of the angles. This is Mahdi's work:
Shapes with same colours are congruent. We can easily note this because all their sides are equal. We can also observe the following:
- We are given that the largest triangle is equilateral
- We also know that the purple triangles are equilateral (each side is $\frac14$ of the [side of the largest triangle]
- The blue triangles are right-angled triangles
- The orange triangles are isosceles triangles
- the green quadrilateral is a trctangle with all angles $90^\circ$
We can complete the angles using the above.
Mahdi and Oscar, Dominic, Olivia, Jodie, Harriet, Rakesh and Mo from Westdene Primary School in the UK worked out the areas of the little shapes, where the area of the smallest equilateral triangle is 1 unit. This is Osacar and Dominic's diagram. They wrote:

We knew that the smallest equilateral triangle is worth one unit. We later knew that the small isosceles triangle and small equilateral triangle when halved had the same area in each half. Therefore the small isosceles triangle was equal in area to the small equilateral triangle.
Rakesh, Mo, Olivia, Jodie and Harriet described the same thing in a different way. This is Rakesh and Mo's work, including their method for the rectangle and the right-angled triangle:
[The areas of the] smallest equilateral triangles and the isosceles [triangles] are equal. You can prove this by placing the two equilateral triangles side by side and the two isosceles also side by side to make two identical rhombuses.
If you place the two smallest equilateral triangles on the width of the rectangle (bases along top and bottom) and the isosceles on the length (bases along left and right) you will find the rectangle to have an area of 4 units.
If you place the smallest equilateral [triangle] and the isosceles [triangle] on the right angled triangles you will find that the right angled triangles are 2 units.
The others used a different method for the rectangle. Olivia, Jodie and Harriet wrote:
A rectangle must be four units because it is double the right angle triangle.
Kevin from Malvern College Hong Kong, Josh and Amara from Westdene Primary School and Julia used a different method to find the areas of the shapes. Julia wrote:
The triangle can be separated in 16 one unit triangles.

Book and Priya from Bangkok Patana School in Thailand were able to find the angles in each of the cut out shapes and they were able to make 15 different trapezia.

Ethan from Meopham Community Academy in the UK and Kevin both found more different trapeziums, parallelograms, rectanges and other quadrilaterals. This is Kevin's work. Notice that Kevin's trapeziums are almost all different to Book and Priya's trapeziums.
These are Ethan's trapeziums and parallelograms.
Ethan found the same rectangles as Kevin, plus these:
Mahdi considered different ways to make rectangles congruent to the little rectangle to try and make a list of all of the possible rectangles. Some of Ethan's are missing from the list, but it is a very good systematic approach. Click here to see Mahdi's working and rectangles.
And Ethan found some other quadrilaterals that are different to any of Kevin's quadrilaterals:
Teachers' Resources
Why do this problem?
This problem can be used in a number of different ways - for students to think about angles, area, or properties of polygons.
Possible approach
Show students the image from the problem, or hand out this worksheet.

"The image was made by taking an equilateral triangle and finding and joining some of its midpoints. Can you work out the angles in the shape?"
Give students a little time to find the missing angles, then discuss the methods they used to work them out.
"Let's imagine that the area of the smallest equilateral triangle is 1 unit. Can you work out the areas of all the other pieces?"
Again, give the class some time to discuss the problem with a partner, and then bring the class together to discuss the reasoning they used to work out how the area of each piece compared with the area of the smallest equilateral triangle.
Next, invite the students to cut the triangle up into the nine smaller pieces to explore the following questions:
- How many different trapeziums (which are not parallelograms) can you make?
- How many different parallelograms (which are not rectangles) can you make?
- How many different rectangles can you make?
- Which other quadrilaterals can you make?
Students could record their working on isometric dotty paper.
As students are working, circulate and listen to their discussions to verify that they understand the properties of trapezia, parallelograms and rectangles. Look out for any examples that not all students have found, and draw attention to them in the final plenary.
Key questions
What angles/areas do you know?
How can you use the angles/areas you know to work out other angles/areas?
What properties does a trapezium/parallelogram/rectangle have?
Possible support
Possible extension
