Finding Circles
Can you find the centre and equation of a circle given a number of points on the circle? When is it possible and when is it not?
Problem

This resource is from Underground Mathematics.
Warm-up
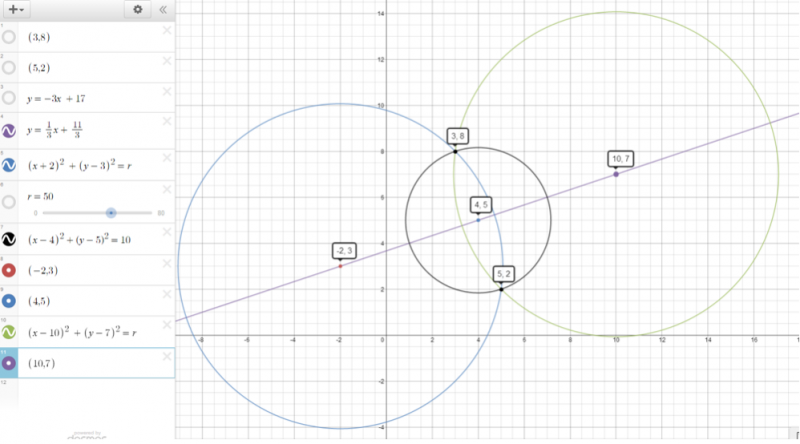
The points $(3,8)$ and $(5,2)$ lie at the ends of a diameter of a circle. What is the equation of the circle?
Some more points...
In the previous question, two points were enough to specify a circle. But is that always the case? For each of the following three statements, is the answer ALWAYS, SOMETIMES or NEVER? Do justify your answers!
You might like to explore your ideas with Geogebra.
- If we specify two (distinct) points in the plane, there is a unique circle that passes through them.
- If we specify three (distinct) points in the plane, there is a unique circle that passes through them.
- If we specify four (distinct) points in the plane, there is a unique circle that passes through them.
Main problem
We now know that given three distinct points in the plane, there is (usually) a unique circle passing through them.
So if we are given three points, we would like to find the equation of the circle that passes through them. How many ways can you find to do this?
Here are some examples for you to try your ideas out on. For each set of three points, find the equation of the circle passing through them.
It is certainly worth sketching a graph to help you understand what is going on in each case!
Which of your approaches is the most effective?
- $A(3,2)$, $B(3,6)$, $C(5,8)$
- $A(0,4)$, $B(4,0)$, $C(-6,0)$
- $A(-1,-5)$, $B(-2,2)$, $C(2,-1)$
- $A(3,3)$, $B(1,-2)$, $C(4,1)$
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Getting Started
An algebraic approach
We want to find an equation of the form $(x-a)^2 + (y-b)^2 = r^2$, where $(a,b)$ is the (unknown) centre of the circle and $r$ is the (unknown) radius. We have $3$ points that lie on the circle, so we
can use these to get some simultaneous equations...
A slightly more geometric way to think about this approach is that we know that the centre, say $(a,b)$, is at an equal distance from all points. So we could write down the distances from $(a,b)$ to our known points, and then equate those...
A geometric approach
If we have two (distinct) points, then there are many circles that
pass through both points. Can you say anything about the centres of
these circles? Might that help us when we know a third point on the
circle?
Student Solutions
Here are Jordan from St Stephen's school's answers to the warm-up:
Since we are told that the points lie on the ends of a diameter of circle, the midpoint of the two points will be the centre of the circle. Therefore the x-coordinate of the centre is $\frac{3+5}{2}=4$ and the y-coordinate of the centre is $\frac{8+2}{2}=5$. Finally, we can find the radius of the circle as the distance between one of the points and the centre which we calculate by pythagoras to be $\sqrt{(5-8)^2+(4-3)^2}=\sqrt{10}$. So in summary the equation of the circle is $(x-4)^2+(y-5)^2=10$.
1. Two distinct points: There is always more than one circle that passes through them. (One thing we can observe is that the centres of such a circle lies on the line that is perpendicular to the line between the two given points, because this is the line of points that are equidistant from both given points - this turns out to be helpful for later)
2. Three distinct points: There is a unique circle through three distinct points, unless the three points are collinear (all lie on a straight line), in which case there is no circle passing through all of them.
3. Four distinct points: There is not always a unique circle that passes through them. Given four random points it is likely that they don't fall on a circle.
Here is a summary of the circle equations you should have found for the main part of the problem:
1. $(x-7)^2+(y-4)^2=20$
2. $(x+1)^2+(y+1)^2=26$
3. $(x+32)^2+(y+32)^2=252$
4. $(x-76)^2+(y-56)^2=14518$
Here are two different approaches that Stephen from St Stephen's school's used to solve the main problem, showing the working for the points given in part 2.
Method 1: Using perpendicular bisectors
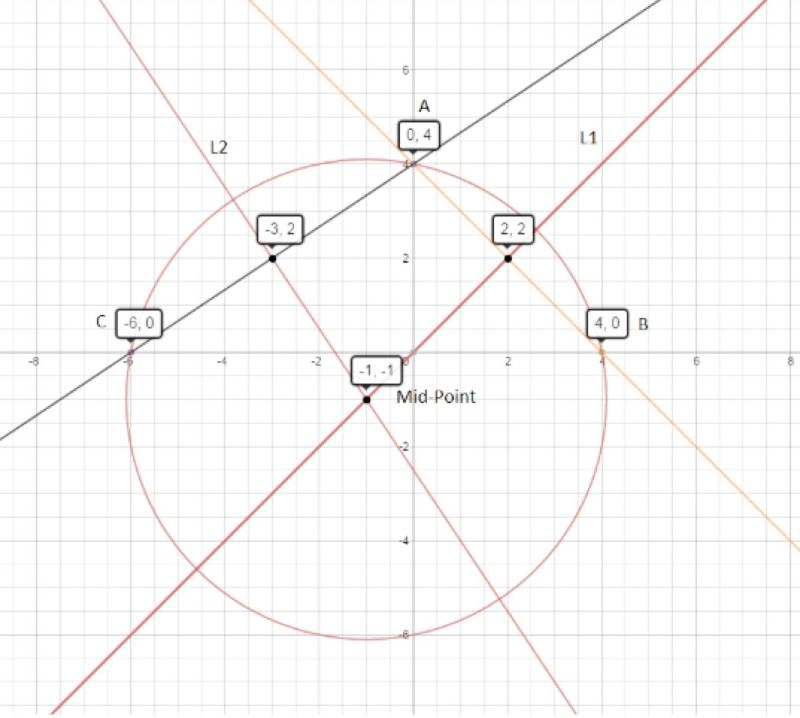
The idea behind this method starts with the observation that Jordan made in part 1 of the warm up:
Given any two points on the circle, the centre of the circle lies on the perpendicular bisector of the line between them, so this means we can find the centre of the circle as the intersection of the perpendicular bisectors of two different pairs of points.
Note that this gives a nice justification for the result in part 2 of the warm up: there is a unique circle between three points unless they are collinear, because there is a unique intersection of two lines unless they are parallel.
For example given the points in part 2: A(0,4) B(4,0) C(-6,0). We first consider the chords AB and AC and find the midpoints:
Mid point = $(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$
Mid point of AB = $(\frac{0+4}{2},\frac{4+0}{2})=(2,2)$
Mid point of AC = $(\frac{0+-6}{2},\frac{4+0}{2})=(-3,2)$
Secondly we find the gradients of these chords:
Gradient = $(\frac{y_2-y_1}{x_2-x_1})$
Gradient of AB $= \frac{0-4}{4-0} =-1$
Gradient of AC $= \frac{0-4}{-6-0} =\frac{2}{3}$
Now we find the corresponding gradients of the perpendicular bisectors of AB and AC, call them L1 and L2 respectively.
Perpendicular gradient $= \frac{-1}{gradient}$
Gradient of L1=$\frac{-1}{-1}=1$
Gradient of L2=$\frac{-1}{\frac{2}{3}} = \frac{-3}{2}$
Now input the midpoints and gradients into the general equation of a line $y=mx+c$ to find the equations of L1 and L2:
L1: $y= mx+c$ so $2=1\times 2+c$ so $c=0$ so the equation of L1 is $y=x$
L2: $y= mx+c$ so $2=\frac{-3}{2}\times -3+c$ so $c=-2.5$ so the equation of L2 is $y=\frac{-3}{2}x-\frac{5}{2}$
So the centre of the circle is where L1 intersects L2 i.e. where:
$x=\frac{-3}{2}x-\frac{5}{2}$
$x=-1$
Substiture the x value into L1 to get that $y=-1$, so the centre of the circle is $(-1,-1)$:
Finally the radius is the distance between the centre and one of the given points:
$r=\sqrt{(0--1)^2+(4--1)^2}=\sqrt{26}$.
Hence in summary the equation of the circle through these points is:
$(x+1)^2+(y+1)^2=26$
Method 2: Simultaneous equations
The second, more algebraic approach, is to substitute the three points into the standard equation of a circle:
$$(x-a)^2+(y-b)^2=r^2$$
and solve the three simultanes equations for r, a and b:
$(0-a)^2+(4-b)^2=r^2$
$(4-a)^2+(0-b)^2=r^2$
$(-6-a)^2+(0-b)^2=r^2$
First we can eliminate r from these equations to get two simultaneous equatoins for a and b:
$(4-a)^2+(0-b)^2=(0-a)^2+(4-b)^2$
$(-6-a)^2+(0-b)^2=(0-a)^2+(4-b)^2$
We can remove all the square terms from both sides and this simplifies to:
$16-8a=16-8b$
$36+12a=16-8b$
which has solution $a=-1, b=-1$, so the centre is $(-1,-1)$
Then substitue back in to find $r=\sqrt{(0--1)^2+(4--1)^2}=\sqrt{26}$, and so the equation of the circle is $(x+1)^2+(y+1)^2=26$ as before.
