The Quintessential Proof
Problem
These first three questions are "warm-ups", designed to introduce the idea. You are welcome to make use of Pythagoras's Theorem as you answer them.
In the following questions, the right-angled triangle has the specific side lengths $6$, $8$ and $10$. Would your answers still be correct if we replaced them with other side lengths, say $a$, $b$ and $c$?
- In the following figure, the red, blue and green regions are all semicircles. How are their areas related?
Image
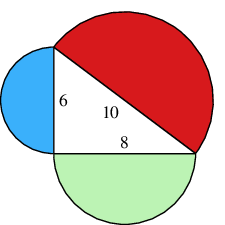
- In the following figure, the red, blue and green regions are all equilateral triangles. How are their areas related?
Image
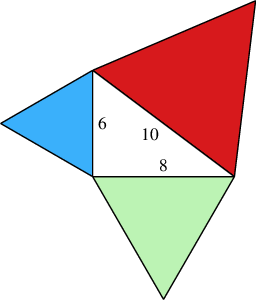
- In the following figure, the red, blue and green regions are all similar triangles. How are their areas related?
Image
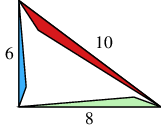
The proof of Pythagoras's Theorem
In this final question, you are asked to use the ideas you have learnt in the earlier questions to prove Pythagoras's Theorem. You may not assume Pythagoras's Theorem to be true when you answer this one!
In the left figure below, the blue and green regions have been formed by dropping a perpendicular as shown. How are their areas related to the red area in the right figure?
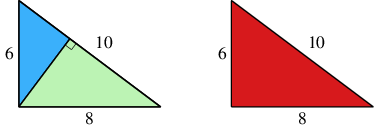
How does this result prove Pythagoras's Theorem?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Here are Melissa's solutions to some of the warm up questions
1. The area of a half circle can be determined by $\frac{{\pi r^2}}{2}$. Therefore each of the areas are as follows:
blue area = $\frac{9\pi}{2}$
green area = $8\pi$
red area =$\frac{25\pi}{2}$
We observe that $\frac{9\pi}{2}+8\pi=\frac{25\pi}{2}$, so the blue and green areas sum to the red area.
More generally if the side lengths are 6,8,10 were replace by a,b and c, the areas are:
blue area = $\frac{\pi a^2}{8}$
green area = $\frac{\pi b^2}{8}$
red area = $\frac{\pi c^2}{8}$
So Green + Blue = $\frac{\pi a^2}{8}+\frac{\pi b^2}{8}$=$\frac{\pi (a^2+b^2)}{8}$. Pythagoras says $a^2+b^2+c^2$ so this simplifies to $\frac{\pi c^2}{8}$ which is the area of the red semi circle, so the same conclusion that blue area + green area = red area holds.
2. The area of a triangle can be determined by $1/2 \times base \times height$.
blue perpendicular height =$\sin (60)\times6 = 3\sqrt{3}$
blue area = $\frac{1}{2} 6 \times 3\sqrt{3}=9\sqrt{3}$
green perpendicular height = $\sin(60)\times8 = 4\sqrt{3}$
green area = $\frac{1}{2} 8 \times 4\sqrt{3}=16\sqrt{3}$
red perpendicular height = $\sin(60)\times10 = 5\sqrt{3}$
red area= $\frac{1}{2} 10 \times 5\sqrt{3}=25\sqrt{3}$
We can see that $9\sqrt{3} + 16\sqrt{3} = 25\sqrt{3}$ so blue area + green area = red area.
Generalising to side lengths of a, b and c:
blue perpendicular height = $\sin(60) \times a = \frac{\sqrt{3} a}{2}$
blue area =$\frac{\sqrt{3} a^2}{4}$
and similarly for b and c.
so again, the green area plus the blue area gives the red area because by pythagoras, $a^2 + b^2 = c^2$.
For the third part Stuart noticed that since the triangles are similar, the ratio of lengths between two of the triangles is constant:
3. Let h denote the perpendicular height of the triangle on the side of length 6, so that the perpendicular heights of the other triangles can be written $\frac{8}{6}h$ and $\frac{10}{6}h$ by similarity. Letting C(b) denote the area of the triangle with base b which is calculated using the formula $\frac{1}{2}\times base \times height$ the areas are calculated as:
$C(6)=\frac{1}{2}\times 6 \times h= 3h= \frac{9}{3}h$
$C(8)= \frac{1}{2}\times 8 \times (\frac{8}{6}h)=\frac{16}{3}h$
$C(10)= \frac{1}{2}\times 10 \times (\frac{10}{6}h)=\frac{25}{3}h$
We observe that $C(6)+C(8)=C(10)$ so the areas add as before.
The same holds more generally for right angled triangle with other side lengths.
Do the areas add whatever the shapes on the side of the triangle are?
Nikhita noticed that the areas don't add when the shapes on the sides of the triangle are rectangles as in the example below.
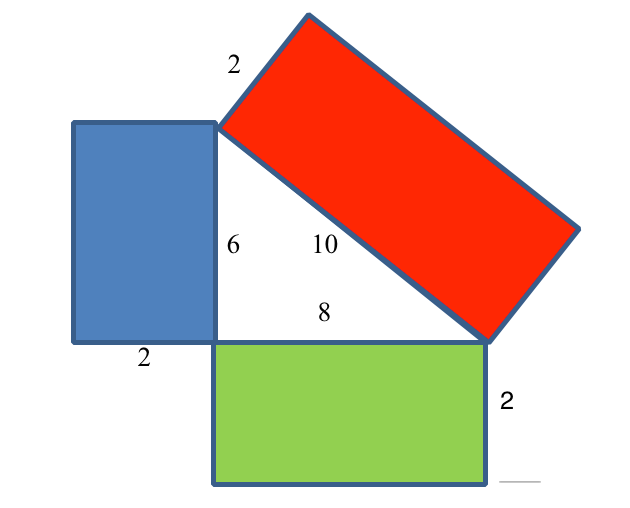
Stuart had the good insight that the areas add whenever the shapes on the side of the triangle are similar.
Kristen also noticed this and gave a neat explanation for why this is always true:
If the shapes on each side of the triangle are all similar then the area of such a shape is proportional to the square of its side length, so the areas of the shapes can be written $\lambda a^2$, $\lambda b^2$ and $\lambda c^2$ for some constant $\lambda$. Pythagoras theorem says that $a^2+b^2=c^2$, so multiplying through by $\lambda$ we get that $\lambda a^2+\lambda b^2=\lambda c^2$ which says the areas of the shapes on the shorter sides add up to the area of the shape on the hypotenuse.
Is there a way we can reverse engineer this to get a proof of Pythagoras' theorem?
Here is Callum's approach for proving pythagoras' theorem, starting with the fact that in this case we know to start with that blue area + green area = red area.
Each of the blue green and red triangles are similar as they have angles of the same magnitude. From this it can be determined that each side of the 2 smaller triangles is related to a side of the larger triangle by an unknown factor (in this case referred to as either n or m). This is shown below.
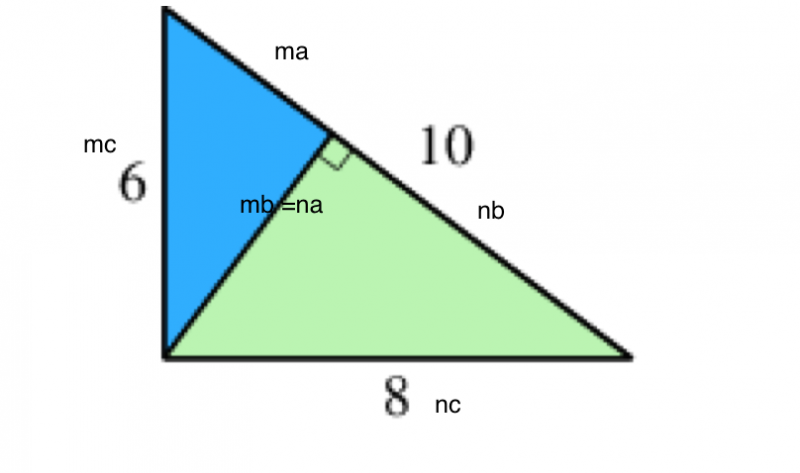
So, using the formula $1/2 \times base \times height$ for the area of a triangle, the areas of the triangles are:
Blue area = $0.5mana = 0.5 n m a^2$
Green area = $0.5nbmb = 0.5 n m b^2$
Red area = $0.5 mc nc = 0.5 n m c^2$
So by the fact that blue area + green area = red area we have that:
$0.5 n m c^2 = 0.5 n m a^2+ 0.5 n m b^2$
which simplifies to pythagoras' theorem.
Kristen has a nice concise proof of Pythagoras' theorem, which is similar to her previous comment but just working backwards:
In this case it is clear from the beginning by looking at the diagram that blue area + green area = red area, since the blue area and green area join together to make the red area.
But also the blue, green and red shapes are all similar because they all contain the same angles. So the areas of the blue, green and red triangles can be written $\lambda a^2$, $\lambda b^2$ and $\lambda c^2$ for some constant $\lambda$.
Substituting these expressions for the areas into blue area + green area = red area, we get that $\lambda a^2+\lambda b^2=\lambda c^2$. Dividing through by $\lambda$ gives Pythagoras' theorem.
So this proof of Pythagoras' theorem is like the reverse of the warm up problems: in the warm up problems we used Pythagoras' theorem to prove that blue area + green area = red area for similar shapes, and here we used that blue area + green area = red area for particular similar shapes to prove Pythagoras' theorem.

