Triangle in a Trapezium
Can you find and prove the relationship between the area of a trapezium and the area of a triangle constructed within it?
Problem
You may find it useful to print off some dotty paper or use the dotty grids environment to explore the first part of this problem.
Triangle in a Trapezium printable sheet - problem introduction
Triangle in a Trapezium printable sheet - starting points
In the two trapeziums below, we have drawn triangles by joining the vertices of one of the non-parallel sides to the midpoint of the opposite side.
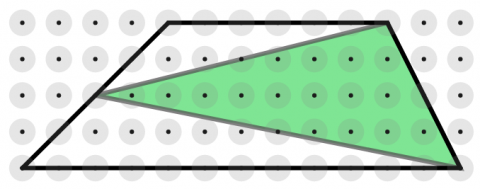

Is there a relationship between the area of each trapezium and the area of the shaded triangle contained within it?
Draw some more trapeziums and construct triangles inside them in the same way. Does the same relationship hold?
Can you find a way to prove that your relationship will always hold for any trapezium?
Once you have had a go at proving it, click below to see some possible starting points.
Can you take each starting point and develop it into a full proof?
Starting Point 1
In this diagram, an extra line has been drawn joining E, the midpoint of AB, to F, the midpoint of CD.

How could you use this diagram to show that the area of the triangle is half the area of the trapezium?
Starting Point 2
Take a look at this sequence of three images. What happens at each stage?



How could you use this sequence of three images to create a proof that the area of the triangle is half the area of the trapezium?
Starting Point 3
Take a look at the image below. Can you see how the trapezium ABCD has been transformed to create this image?

How could you use this image to prove that Triangle CED has half the area of Trapezium ABCD? Click below to show two more images that might help.


Getting Started
For each of the starting points, it might be a good idea to label some of the side lengths and heights with letters. The letters used below correspond to those used in each starting point in the problem.
Starting Point 1
How would you work out the area of the two unshaded triangles? You might need to choose some letters to represent certain quantities...
Using the same letters, can you work out the area of the trapezium?
Starting Point 2
How does triangle BEG compare with triangle AEF? How do you know?
How do we know that triangle CED and triangle CFD have the same area?
Starting Point 3
The trapezium has been rotated $180^{\circ}$ around F.
Can you prove that ABGH is a parallelogram? It might help to mark angles that you know are equal, and angles that you know add up to $180^{\circ}$.
Student Solutions
Thank you to everyone who sent in their solutions to this problem. We received either full or partial solutions from Sammy at Lancing College; Tobias and Ana (no schools given); Sanika from PSBBMS in India; and Quang from the British Vietnamese School in Vietnam. As you discovered, there were several ways to prove this result and we suggested three possible approaches.
Method One
For this method, we suggested drawing an extra line joining E and F, the midpoints of AB and CD respectively.
Several of you suggested that it would be helpful to explore another relationship before going any further. For example, Sanika noted the usefulness of exploring "a relationship between the lengths of BC, EF and AD and also figure the heights of the two smaller trapeziums."
Well spotted, Sanika and everyone else who realised that this would be useful. This relationship, which several of you uncovered in different ways, is known as the mid-segment theorem for trapezia and it can be very helpful for Method 1. It states that if a line connecting the midpoints of the two legs of a trapezium is parallel to the bases, then its length is equal to half the sum of the lengths of the bases.
Sammy, from Lancing College, made good use of this theorem in this solution:

Method Two
Well done to everyone who followed the sequence of images to explore Method Two.
Here's how Sanika approached the problem using Method 2:
To prove that the resultant figure GCDF is a parallelogram, we would have to prove that the triangles EAF and EBG are congruent.
AE = BE (as E is the midpoint of the line segment AB)
Angle GEB = Angle FEA (Vertically opposite angles)
GB and AF would be parallel as they are extensions of parallel lines. Therefore, we can say that angle GBE = angle FAE as they are alternate-interior angles.
Therefore Triangle EAF is congruent to triangle EBG.
This implies that the area of the trapezium is the same as the area of the parallelogram.
We can then invert the parallelogram so that the base and height of both the parallelogram and the triangle would be the same measure.
Let base be 'b' and let the height be 'h'.
Therefore the area of the parallelogram = bh
Area of the triangle = bh/2
Since the area of the parallelogram is the same as the area of the trapezium we can say that the triangle is half the area of the trapezium.
Method 3
Here's Sanika's sketch:

Have you noticed how Sanika has annotated our original diagram to help her solve the problem? A good sketch is always worth the time spent on it.
From the diagram, we can tell that the line segment BG will be equal to line segment AH. They will also be parallel as opposite sides of a Trapezium are parallel. Since we have one pair of opposite sides which are parallel and equal, we can deduce that the quadrilateral ABGH is a parallelogram.
Once she was convinced that the shape was a parallelogram, Sanika followed the hints provided for Method 3:
As opposite angles of a parallelogram are equal, the following will hold true:
Angle B = Angle H
Angle A = Angle G
Using the SAS [side-angle-side] congruence criteria, we can say the following:
Triangle EAD is congruent to triangle JGC (Thus, line segment ED = JC)
Triangle CBE is congruent to triangle DHJ (So line segment CE = DJ).

We can then rearrange triangles CBE, CGJ, AED and DHJ, as shown in the image above, to form the quadrilateral DECJ (or CJDE).
Since AE and HJ are of the same length 'x', we can join them together.
Similarly as BE and GJ also share a length of 'x', we can join them together.
As proved earlier, triangle EAD is congruent to triangle JGC and triangle CBE is congruent to triangle DHJ so the bases will be the same, in which case we can join them to form the quadrilateral DECJ. This is identical to the two triangles contained in the trapezium, put together.
Therefore, we can say that the area of the quadrilateral DECJ is half the area of the parallelogram BGHA.
As the parallelogram is just 2 copies of the trapezium, we can say that the area of CED is half the area of the trapezium ABCD.
Well done to Sanika and everyone else who explored this problem. We hope you enjoyed investigating different approaches towards finding a solution.
Teachers' Resources
Why do this problem?
Students often think that there is only one correct way to approach a geometrical challenge. In this problem, students have the opportunity to discover a geometrical relationship, and then explore three starting points that lead to different methods to prove the relationship always holds. Along the way there's a chance for some "purposeful practice" at finding the area of triangles and trapezia.
Possible approach
Students may find it useful to work on dotty paper or use the dotty grids environment to explore the first part of this problem.
Start by showing the two trapeziums below, and explain that the triangles join the vertices of one of the non-parallel sides to the midpoint of the opposite side.


Invite students to work out the area of each trapezium and shaded triangle, and then discuss how they worked out the areas. Then ask them to draw some more trapeziums and construct triangles inside them in the same way. After everyone has had time to create some examples, collect together their results in a table on the board.
"What do you notice about the area of the triangle compared with the area of the trapezium?"
"It's always half the area!"
Invite students to think about how they could prove that the area of the triangle is always half the area of the trapezium. After they have had some time to think about it, you could hand out this worksheet: Triangle In a Trapezium. Challenge them to take each starting point and turn it into a complete justification. There are three different starting points so each group could work on a different starting point and then present the complete proof to the whole class. Finally, take time to discuss which method they found most convincing or appealing, and why.
Key questions
Starting Point 1
How would you work out the area of the two unshaded triangles?
Does it help to choose letters to represent some of the lengths and heights?
Using the same letters, can you work out the area of the trapezium?
Starting Point 2
How does triangle BEG compare with triangle AEF? How do you know?
How do we know that triangle CED and triangle CFD have the same area?
Starting Point 3
Can you prove that ABGH is a parallelogram?
Does it help to mark angles that you know are equal, and angles that you know add up to $180^{\circ}$?
Possible support
To scaffold the step from particular cases to the general proof, invite students to create the images from each Starting Point on dotty paper for trapezia that they have already explored. Then encourage them to adapt the reasoning from their numerical examples to prove the general case.
Possible extension
Kite in a Square is a more challenging geometrical problem which offers three different jumbled up proofs for students to sort out.
