Penta Post
Problem
Here are the prices for 1st and 2nd class mail within the UK [in 2002].
| Weight up to | First Class | Second Class |
|---|---|---|
| $60g$ | $27p$ | $19p$ |
| $100g$ | $41p$ | $33p$ |
| $150g$ | $57p$ | $44p$ |
| $200g$ | $72p$ | $54p$ |
| $250g$ | $84p$ | $66p$ |
| $300g$ | $96p$ | $76p$ |
| $350g$ | $ £1.09$ | $87p$ |
| $400g$ | $ £1.30$ | $ £1.05$ |
| $450g$ | $ £1.48$ | $ £1.19$ |
| $500g$ | $ £1.66$ | $ £1.35$ |
| $600g$ | $ £2.00$ | $ £1.60$ |
| $700g$ | $ £2.51$ | $ £1.83$ |
| $750g$ | $ £2.69$ | $ £1.94$* |
| $800g$ | $ £2.91$ | |
| $900g$ | $ £3.20$ | |
| $1kg$ | $ £3.49$ |
Costs for First Class items over $1kg$ are $ £3.49$ and then $85p$ for each extra $250g$.
*Items over $750g$ cannot be sent second class.
You have an unlimited number of each of these stamps:
Image

|
Image

|
Image

|
Image

|
Image

|
Image

|
|
$4p$
|
$10p$
|
$19p$
|
$27p$
|
$37p$
|
$ £1.00$
|
Reproduced by kind permission of Consignia plc. All rights reserved.
1/ Which stamps would you need to post a parcel weighing $825g$?
2/ I want to send a package 1st class which weighs $235g$. It is very small so I want to use as few stamps as possible. Which ones would I use?
3/ If I only had $3$ of each kind of stamp, which $2$nd class price could I not make?
4/ How many different combinations of stamps could be stuck on a letter weighing $140g$ if it goes 1st class?
5/ I use the following stamps to send two items, one 1st class and the other 2nd class:
Image

|
Image

|
Image

|
Image

|
Image

|
Image

|
Image

|
What could their weights be?
Further extension to this activity can be carried out by considering the value of the stamps alone, as numbers $4$, $10$, $19$, $27$, $37$ & $100$. For example taking the $5$ lowest numbers [missing out the $100$] challenging the pupils to come up with the smallest number of ways you can get totals between $4$ and $50$. This could lead to questions about what totals can NOT be had, and checking to see if you've really got the smallest number of ways, each time.
All tables reproduced by kind permission of Consignia plc. All rights reserved.
UK folk need to be aware that all this has changed since 2009 ! (See Royal Mail)
Getting Started
It may be helpful to write out the different combinations of stamps that could be used for each price.
Student Solutions
Martha from Tattingstone School sent us a very clearly answer to the first part:

Martha goes on to give the solution for
the second part too: 
Caroline, also from Tattingstone, has
answered the third part of the problem: 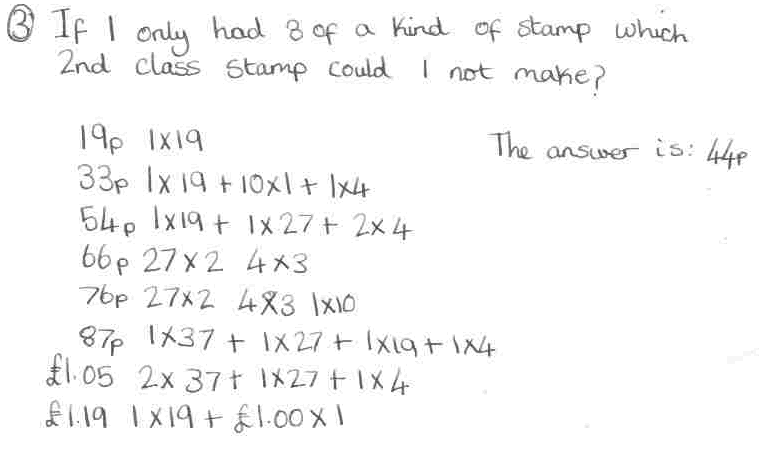
Well done Caroline - although perhaps it
would have been better to write 3 x 4, not 4 x 3. Back to Martha
for part four: 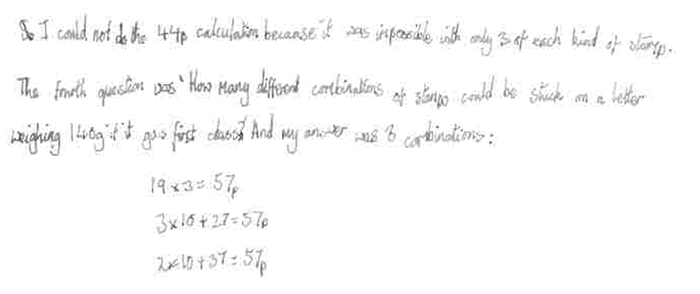
Finally, Caroline has answered the last
part for us: 
Excellent answers both of you! Very well done.
