Can You Find ... Asymptote Edition
Given a sketch of a curve with asymptotes, can you find an appropriate function?
Problem
Can you find a function that gives the following picture?
Image
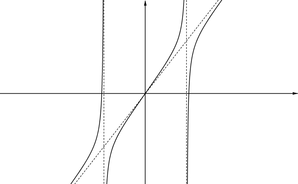
You can use Desmos to help you construct your function.
This is an Underground Mathematics resource.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Getting Started
Here are some things to think about...
(a) What does a curve with real roots look like algebraically?
(b) What does a curve with vertical asymptotes look like algebraically?
(c) What function does the middle portion of the picture remind you of?
(d) What is happening to $f(x)$ for large, respectively small, values of $x$?
(a) What does a curve with real roots look like algebraically?
(b) What does a curve with vertical asymptotes look like algebraically?
(c) What function does the middle portion of the picture remind you of?
(d) What is happening to $f(x)$ for large, respectively small, values of $x$?
Student Solutions
Aneesh from West Island School Hong Kong, Louis from EMS, and Emily from Doctor Challoner's High School submitted solutions to this problem.
Aneesh first found that $\frac{x^3-4x}{x^2-1}$ produced a graph of this shape, and then generalised his findings:
Functions of the form $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$ where $a>b$ seem to obey the general shape of the displayed graph.
In order to work this out, I first considered the asymptotes on the graph. The function seemed to have two vertical asymptotes, evenly spaced from $0$ which I originally thought were at $x=1$ and $x=-1$. So I knew that the denominator of my rational function should have roots at 1 and -1.
Furthermore I considered the limits as $x$ approached $0$,$1$,$-1$ and infinity of the function shown. I knew that the limit as $x$ approached positive infinity of the function was an oblique asymptote (that looked like the line $y=x$).
The limit as x approached $1$ from the right hand side was negative infinity, and so I knew that the numerator must be negative for $x$ close to but greater than $1$.
By symmetry, I knew that my numerator must be positive for $x$ close to but less than $-1$ from the LHS.
Keeping this in mind, I then considered the roots of my function. They were $0$, a number greater than $1$ (greater than my positive vertical asymptote) and a number less than $-1$, (less than my negative vertical asymptote). So the roots of my numerator were $0$, $2$, $-2$. So I initially wrote down $x(x+2)(x-2)$ for my numerator. This numerator even satisfied my previously imposed conditions, because if I pick an $x$ value close to but greater than $1$, I will get a negative value on my numerator. And if I pick an x value close to but less than $-1$, I will get a poitive value in my numerator. This is because $(x-2)(x)$ would always yield negative, the product of two negative numbers is a positive.
So in general, the form of such a function would be $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$. Moreover, on taking the limit to negative or positive infinity of the expression chosen above, as the numerator is a polynomial of degree one greater than the polynomial below, the function gets closer and closer to $\frac{x^3}{x^2} = x$. Which yields the oblique asymptote.
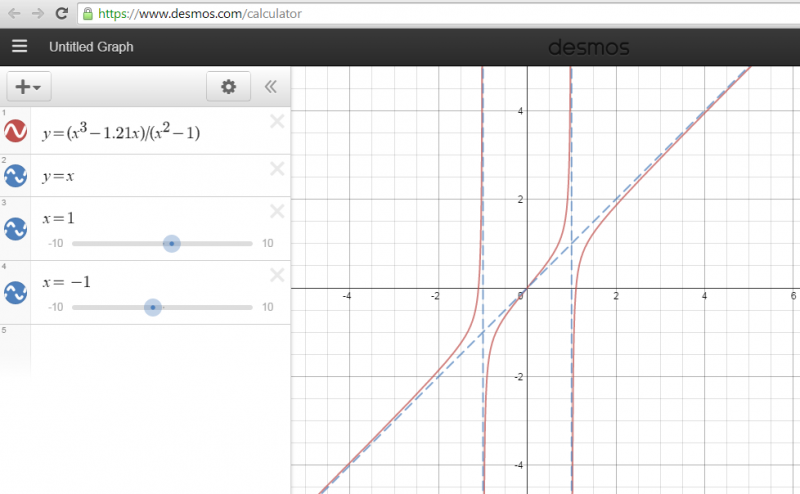
Louis thought similarly about general polynomial functions which produce this graph, and decided on the function $\frac{x^3-1.21}{x^2-1}$. Below is a picture of his graph in Desmos:
Emily also thought about general polynomial functions which produce graphs of this shape, and went on to think about whether it was possible to produce this graph using trigonometric functions. Here is a link to her solution.
Thank you everybody!
Aneesh first found that $\frac{x^3-4x}{x^2-1}$ produced a graph of this shape, and then generalised his findings:
Functions of the form $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$ where $a>b$ seem to obey the general shape of the displayed graph.
In order to work this out, I first considered the asymptotes on the graph. The function seemed to have two vertical asymptotes, evenly spaced from $0$ which I originally thought were at $x=1$ and $x=-1$. So I knew that the denominator of my rational function should have roots at 1 and -1.
Furthermore I considered the limits as $x$ approached $0$,$1$,$-1$ and infinity of the function shown. I knew that the limit as $x$ approached positive infinity of the function was an oblique asymptote (that looked like the line $y=x$).
The limit as x approached $1$ from the right hand side was negative infinity, and so I knew that the numerator must be negative for $x$ close to but greater than $1$.
By symmetry, I knew that my numerator must be positive for $x$ close to but less than $-1$ from the LHS.
Keeping this in mind, I then considered the roots of my function. They were $0$, a number greater than $1$ (greater than my positive vertical asymptote) and a number less than $-1$, (less than my negative vertical asymptote). So the roots of my numerator were $0$, $2$, $-2$. So I initially wrote down $x(x+2)(x-2)$ for my numerator. This numerator even satisfied my previously imposed conditions, because if I pick an $x$ value close to but greater than $1$, I will get a negative value on my numerator. And if I pick an x value close to but less than $-1$, I will get a poitive value in my numerator. This is because $(x-2)(x)$ would always yield negative, the product of two negative numbers is a positive.
So in general, the form of such a function would be $\frac{(x)(x+a)(x-a)}{(x+b)(x-b)}$. Moreover, on taking the limit to negative or positive infinity of the expression chosen above, as the numerator is a polynomial of degree one greater than the polynomial below, the function gets closer and closer to $\frac{x^3}{x^2} = x$. Which yields the oblique asymptote.
Louis thought similarly about general polynomial functions which produce this graph, and decided on the function $\frac{x^3-1.21}{x^2-1}$. Below is a picture of his graph in Desmos:
Image

Emily also thought about general polynomial functions which produce graphs of this shape, and went on to think about whether it was possible to produce this graph using trigonometric functions. Here is a link to her solution.
Thank you everybody!

