Guess My Quad
How many questions do you need to identify my quadrilateral?
Problem
Here is a game you could play with a friend...
Ask your friend to choose one of the shapes, and then try to identify which it is.
Your friend can only reply "Yes" or "No" to your questions.
Then swap over.
Who can identify the other's shape with the fewest questions?
Image
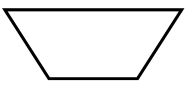
| Image

| Image
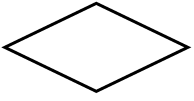
| Image
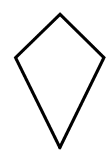
|
| Isosceles trapezium | Rectangle | Rhombus | Kite |
Image
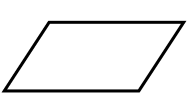
| Image
| Image
| Image
|
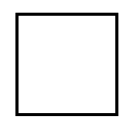
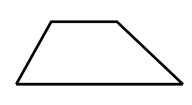
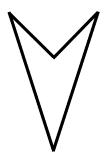
| Parallelogram | Square | Trapezium | Arrowhead |
You may wish to print out this sheet to record the answers and help you eliminate possible shapes or use this interactivity to organise the quadrilaterals.
Here are some questions you might like to consider:
How many questions do you need to ask to guarantee you know your friend's shape?
What would you ask first?
If your friend says "Yes", what would you ask next?
If your friend says "No", what would you ask next?
Charlie says he can always identify Alison's shape after asking just three questions.
Which question might Charlie ask first? Which follow-up questions might he then ask?
Can you invent a game with more shapes, where you can always identify your friend's shape in four questions? What is the maximum number of shapes you could have in such a game?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
When I play "Think of a number" trying to identify a number between 1 and 100, I can start by asking:
"Is it 52?" or "Is it less than 5?", but I usually choose to ask
"Is it even?" or "Is it greater than 50?"
Can you see why I prefer the second set of questions?
Can you find similar questions to ask for "Guess my Quad" game?
Student Solutions
Many thanks to all of you who submitted solutions to this problem: you've used several different methods. Many of you used flow charts to present your solutions, which made it very easy to see what questions you were asking depending on the answers to your previous questions.
Mariah, Georgia and April, from Hastings Secondary College, Australia, submitted this solution. They used the fact that their kite and arrowhead had right angles in them to arrange their questions.
These are their shapes, and their questions that they would ask:


Nathan, from Bishop Wordsworth's School, explained why three questions was the minimum that you would need to be able to work out what the quadrilateral is:
I realised that to get the smallest result, each question asked would have to halve the number of shapes left until you have the final shape. Therefore, the minimum amount of questions you could ask and certainly get a right answer is three: $8 \div 2 = 4$; $4 \div 2 = 2$ and $2 \div 2 = 1$, which makes a total of 3 questions.
He was also able to find a way to work out the shape using only three questions. He was able to do this without assuming any extra properties of the shapes:
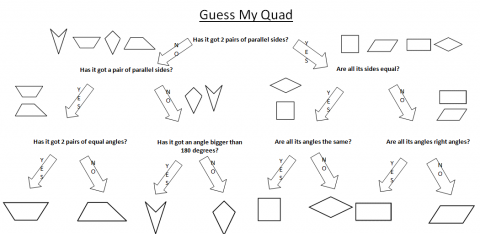
Zach also had a flow chart to show his method:



Thank you and well done to everyone who submitted a solution.
Teachers' Resources
Why do this problem?
This problem gives students the opportunity to derive the various properties of quadrilaterals whilst reinforcing the importance of using appropriate language and terminology. These may include angle rules, identifying parallel lines and symmetry which could lead to solving more complex questions. Along the way, the challenges will provoke some insightful discussion linking together different geometrical ideas.
Possible approach
The task could be used when students are not yet familiar with these quadrilaterals (they can be labelled a-h), but they should be familiar with right angles, parallel lines and symmetry. Students could play the game in pairs or begin by playing as a whole class against you. You could use the interactivity to sort and eliminate quadrilaterals to support this discussion. Students should hone their strategies in pairs or small groups, which will involve defining each shape based upon its characteristics. Encourage students to use correct mathematical language in these discussions.
You might want to move on to the questions to consider at the bottom of the problem.
The task could also be used as a whole-class plenary exercise. You can think of a quadrilateral and select students to ask questions, again encouraging use of correct mathematical language and the interactivity may help to support this discussion.
It may be useful to print and cut out the shapes so that students can label and group them more easily. Alternatively, the quadrilaterals could be displayed on the board. Students' thinking could be brought together by groups presenting their findings, for instance posters of their flow charts. There is also room for a whole-class discussion using the key questions for prompts to extend their ideas further.
Encourage students to play the game without using the handout. Can they remember the shapes and their properties without looking at them?
Key questions
- Who has found the shape after the smallest number of questions?
- What are ‘good’ and ‘bad’ questions?
- How many questions do you need to ask to guarantee you know your friend's shape?
- If your friend says "Yes", what would you ask next? If your friend says "No", would you still ask the same question?
- Charlie says he can always identify Alison's shape after asking just three questions. Which question might Charlie ask first? Which follow-up questions might he then ask?
- Can you string the eight special quadrilaterals in a line with just one difference between them?
Possible support
Initially, the students could be prompted to note the properties of each quadrilateral under given headings after being taught the relevant concepts. An activity whereby students fill in a table could be useful (see below for example). This could be followed by a grouping exercise to sort the shapes providing a starting point as to how they can be distinguished from one another.
Shape | # of right angles | # of pairs of parallel lines | # lines of symmetry | # sides of equal length |
Isosceles Trapezium |
|
|
|
|
Rectangle |
|
|
|
|
Kite |
|
|
|
|
Rhombus |
|
|
|
|
Parallelogram |
|
|
|
|
Square |
|
|
|
|
Trapezium |
|
|
|
|
Arrowhead |
|
|
|
|
Additionally, students could each be given a single shape to work with and asked to label various features. They could compare this with their peers to initiate collaboration.
Possible extension
Can you invent a game with more shapes, where you can always identify your friend's shape in four questions? What is the maximum number of shapes you could have in such a game?
