Lost books
Problem
While we were sorting some papers we found $3$ strange sheets which seemed to come from small books. They had once been used for wrapping and one side was very faded. The other side was in a language we did not know, but there were page numbers at the foot of each page.

Did the pages come from the same book, we wondered, and what numbers had been on the other sides of the sheets?
I decided to make a little book to see how the numbers worked. It had $4$ sheets which I folded to make $16$ pages. There was no need to staple it.
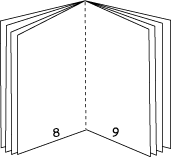
Then I made other little books, with both more and fewer pages. I made a table of my results and soon I knew how the numbering worked and could answer my own questions.
What answers do you think I got?
Later we found another sheet. The numbering on this was a bit different. Can you work out why?

Getting Started
Student Solutions
Here is one way to think about this numbering problem. This came from James and Kirsty. There are many other ways to look for patterns (although drawing a table can help).
For the first part (with the sheet with 8 and 21), the book had a total of 28 pages on 7 sheets of paper.
First I noticed that with four sheets, page 8 is next to page 9 as in the picture. Then I noticed that if you add a sheet, there are an extra four pages in between page 8 and the page opposite, which will be page 13. I then made this table:
| Number of sheets | Number of page next to page 8 |
| 4 | 9 |
| 5 | 13 |
| 6 | 17 |
| 7 | 21 |
| 8 | 25 |
For the second part, I used a similar pattern. I started by noticing that with 9 sheets, page 36 will be the back page and will be opposite page 1. I then considered adding pages to the outside of the book. Each time you do this, the number of the page opposite page 36 increases by 4.
| Number of sheets | Number of page next to page 36 |
| 9 | 1 |
| 10 | 5 |
| 11 | 9 |
| 12 | 13 |
| 13 | 17 |
| 14 | 21 |
| 15 | 25 |
Well done for noticing this! One way toget this numbering would be to start numbering on the inside cover. Why not try making your own numbering puzzles?
Teachers' Resources
Why do this problem?
This problem requires learners to work systematically and use logical thinking about numbers. Much of it can be done practically which opens up possibilities for different types of learning. It could be very useful for getting learners to develop rules for how something works.Key questions
Possible extension