11x11 Square
Problem
There's an interesting trick you can do with an $11 \times 11$ square...
It's possible to make five rectangles, each with different widths and lengths, using each of the following dimensions once only: $1, 2, 3, 4, 5, 6, 7, 8, 9, 10$, that can be used to tile the $11 \times 11$ square!
Convince yourself that only one of the arrangements below could satisfy these conditions.



Can you find the dimensions of the five rectangles which can tile the $11 \times 11$ square?
Can you find all the possible different solutions?
Here different means not a reflection or rotation of another solution.
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
For the initial question:
Are any rectangles too long?
Do any rectangles share the same width or height?



For the final question:
What must the areas of the five rectangles add up to?
Student Solutions
JQ Lim from Malaysia, Neel from Zurich International School in Switzerland and Year 5 from Wellington College Shanghai in China explained why only one of these diagrams is a possible solution. JQ Lim wrote:



From the first shape you can see that it wouldn't work already as the length of the yellow rectangle is the width of the square, meaning it is 11, and it wouldn't satisfy the conditions. The third shape also wouldn't work as you can see the green and pink triangle has the same width.
Therefore, it means that the third one is the only possible situation. And as you can see from the shape, no sides are the same/take up one whole side of the square.
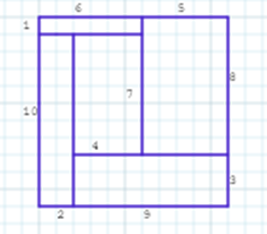
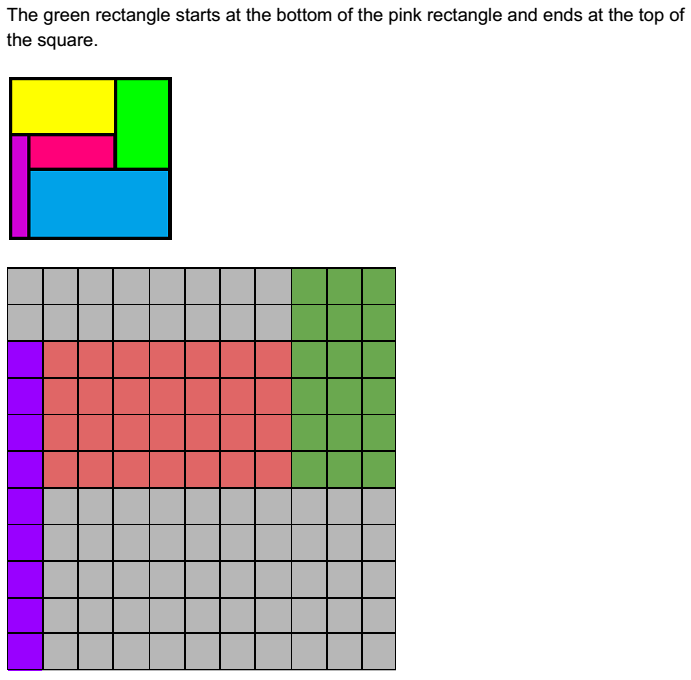
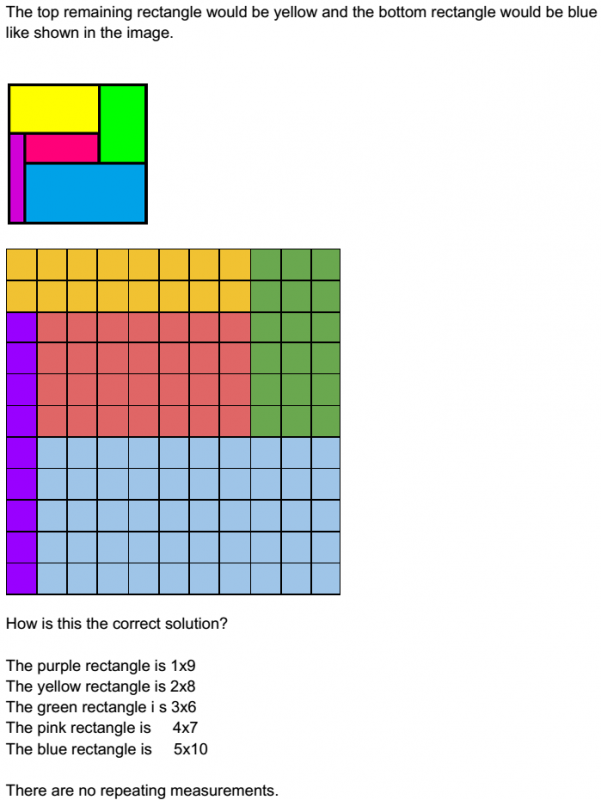
Year 5 from Wellington College Shanghai inspected the middle diagram to work out which lengths were which:

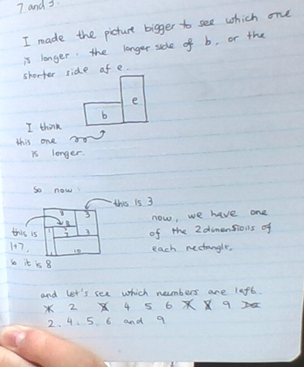
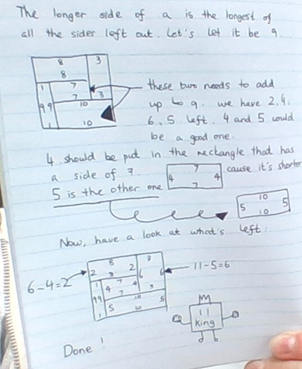

Sophie and the LMS puzzle club at The Lady Margaret School in the UK JQ Lim both found solutions that were the same as Year 5's second solution. JQ Lim used a different method:
Originally, I had spent very long doing trial and error (it seemed to be the only way).
Firstly, I tried to narrow it down using the fact that the area was 121 and certain heights had to be odd, even, etc. to make an odd number (121).
From there, I trial and error two things: areas that could make 121, and how those lengths could fit on an 11x11 square.
But this took a long time and I realized I could do it another way.
Just trial and error lengths that could go on an 11x11 square.
However, this also took a long time, so I decided to stop, asked for a hint and try a different way.
Looking at the shapes in part 1, I found out that
the maximum number of rectangles you can have making up one side of the square is 2. If you had 4, one rectangle could not make up one whole other side, as the length of its sides cannot exceed 10.
It also cannot have three on one side. As shown by the first rectangle, the only way to get 5 rectangles while still having three one side, is to have one rectangle that has a length of 11. You could then try to shorten the three rectangles, but it would mean you cannot form a rectangle from the remaining space that is left.
Now that I know this, I also know since one side of the square is 11, that means the rectangles that form it are either of one of these five widths:
1,10
2,9
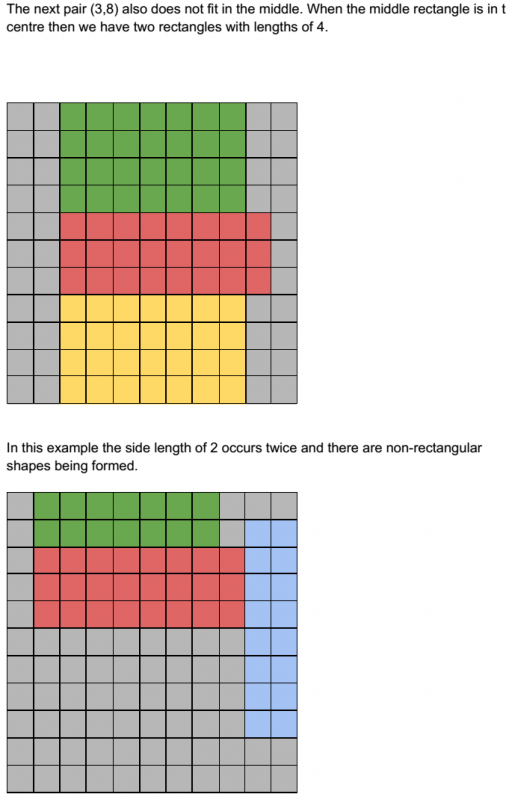
3,8
4,7
5,6
And since there are five of them, the remaining one will form the rectangle in the middle!
In addition, I also found out from my previous attempts at trial and error that it doesn't matter which four rectangles on the outside to decide what your lengths could be.
If you turn the shape around, you notice that it has the same pattern either way, meaning it is a reflection of one another and it is unnecessary to check if a certain dimension works on other rectangles.
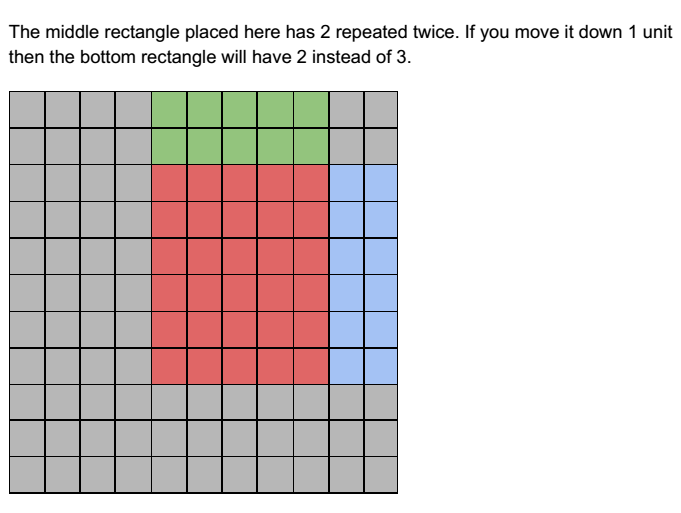
However, the only exception is the middle rectangle. If you change it changes the whole shape.
Therefore, I would still trial and error, but in a much more limited way. I would now just trial and error with the middle rectangle being one of the five dimensions listed above.
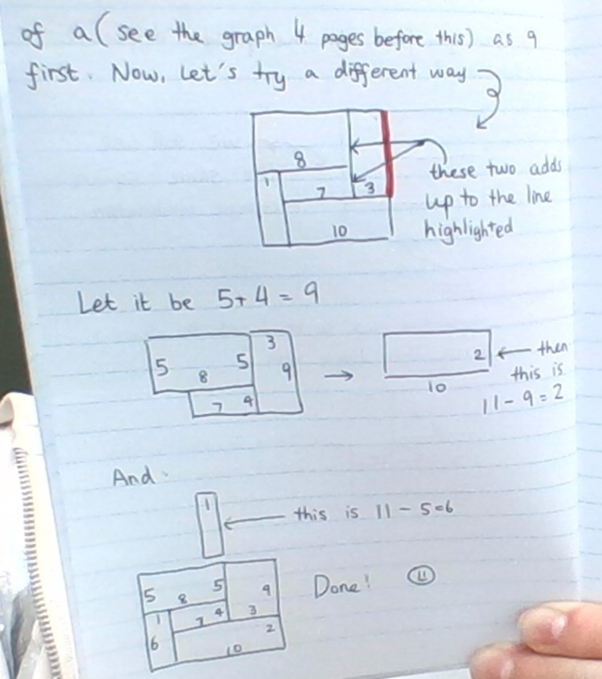
I discovered that only this solution works!
Tips:
- Always try to narrow down your trial-and-error options
- If one way doesn’t work, and you’ve been doing it for a long time, and you keep pushing, it’s probably the wrong way, so just stop. Do it another way or get a hint
Neel used a similar (but different) method to find Year 5's first solution:







Can we be sure that these two are the only two solutions?
Teachers' Resources
Start by asking students to consider which of the three diagrams could be a possible solution, and discuss the reasons why the other two are not possible.



Some possible questions are:
- In the first diagram, what can you say about the yellow rectangle (the one at the bottom)?
- In the first diagram, what do the red and green rectangles have in common?
Ask students to draw possible arrangements of five rectangles that avoid any two of them having the same height or width.
Some further questions:
- Is it possible to have a rectangle with length $9$ in the centre of the diagram?
- What about one with length $8$?
- How many ways can you write $11$ as the sum of two positive integers?
- What must the areas of the five rectangles add up to?
This problem featured in the NRICH Secondary webinar in April 2022.
