Difference of Two Squares
What is special about the difference between squares of numbers adjacent to multiples of three?
Problem
Difference of Two Squares printable worksheet
You may wish to look at the problem What's Possible? before trying this one.
Choose a number in the $3$ times table. Take the numbers on either side of your chosen number and find the difference between their squares.
Try it a few times. What do you notice?
Can you prove it will always happen?
Choose a number in the $5$ times table.
Take the numbers on either side of your chosen number and find the difference between their squares.
Try it a few times. What do you notice?
Can you prove it will always happen?
Is there a similar relationship for other times tables?
Extension
Instead of taking the numbers on either side of your starting number, investigate what happens if you take the numbers two above and two below your starting number and then work out the difference between their squares...
If you enjoyed this problem you may like to try Why 24? next.
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
You may want to take a look at Pair Products - it is a similar problem but offers a little more structure and support.
Student Solutions
Darius from Victoria College in the Channel Islands and Maisy from Long Field Academy in England noticed that, when using the 3 times table, the difference is a multiple of 3. Maisy wrote:
3 (3 times table):
22 = 4
42 = 16
16 $-$ 4 = 12
12 is in the 3 times table because 4 $\times$ 3 = 12
Sanika from India and Sarvitha from The Ellen Wilkinson School for Girls, James from High Storrs School and Alex from Long Field Academy, all in the UK, noticed that this always gives a multiple of 12. This is Sarvitha's work:
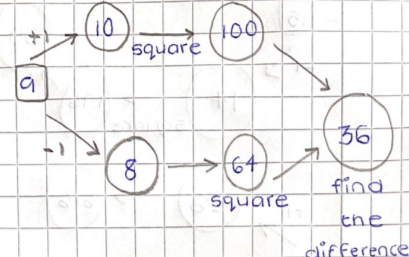


They are all multiples of 12
Sarvitha proved this result by writing $3n$ for any multiple of 3:
Elissa from The Ellen Wilkinson School for Girls, James, Darius, Sanika and Alex all noticed and proved something slightly different. This is Alex's work:
The pattern is that your answer will always be 4 $\times$ your initial number.
I can prove this because:
In the 3 times table: $x$ = the number you times by $3.$
e.g. If $x = 1,$ chosen number [in the 3 times table] is $3,$
If $x = 2,$ chosen number is $6$
The numbers in the sequence are
$(3x -1), 3x, (3x+ 1)$
$(3x + 1) (3x + 1) -((3x-1) (3x-1)) = 9x^2 + 6x + 1 - (9x^2- 6x +1) = 12x$
Which is 4$\times$3$x$, so 4$\times$ the number in the 3 times table.
For numbers in the 5 times table, Darius noticed and proved that the difference between the squares is always a multiple of 5:
Let $5n$ be a multiple of $5, n \in \mathbb{N}, n \gt1$
$\therefore$ difference of squares of numbers on either side is equal to: $$\begin{align} (5n+1)^2 &- (5n-1)^2\\
= 25n^2+10n+1 &-(25n^2-10n+1)\\
= 20n\end{align}$$
$\dfrac{20n}{4} = 5n \therefore 20n$ is a multiple of $5$
Alexis from Long Field Academy, James and Sarvitha noticed that they are in fact multiples of 20. In fact, you can see this from Darius' proof.
Once again, Alex proved that the difference is always 4 times the original multiple of 5. The proof is actually the same as Darius' proof that the difference is $20n,$ because $20n = 4\times 5n$ which is 4 times the original multiple of 5.
What about different times tables? Maisy from Long Field Academy wrote:
Whatever times table the first number you picked comes from, the number you
end up with is in it. For example:
12 (6 times table):
11 squared = 121
13 squared = 169
169 $-$ 121 = 48
48 is in the 6 times table because 8 $\times$ 6 = 48.
Darius and Sanika proved it. This is Darius' proof:
Let $\alpha n$ be a multiple of $\alpha$ (this is the same step as before, just with the $\alpha$ times table, rather than the $3$ or $5$ times table).
$\therefore$ difference of squares of numbers either side is: $$\begin{align} (\alpha n+1)^2 &- (\alpha n-1)^2\\
= \alpha^2n^2+10n+1 &-(\alpha^2n^2-10n+1)\\
= 4\alpha n\end{align}$$ Dividing by $\alpha$, which is the times table:
$\dfrac{4\alpha n}{\alpha} = 4n \therefore 4\alpha n$ is a multiple of $\alpha $
Louis from the UK tried numbers in the 7 times table:
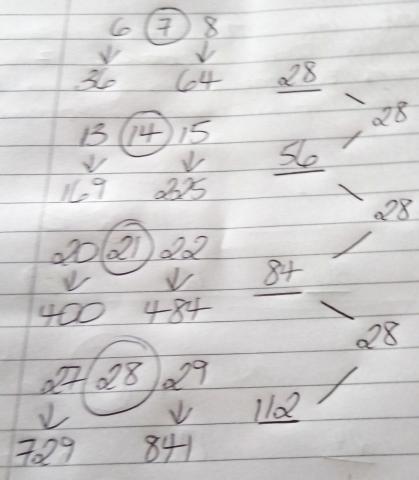
Holly from Long Field Academy noticed something else familiar:
If you pick a number and multiply it by 4 this is equal to the difference between the squares of the numbers either side of your chosen number.
e.g. If I chose the number 18 and multiply this by 4 you will get 72.
The squares of 17 and 19 are 289 and 361; the difference between 361 and 289 is 72.
James, Alex and Elissa all proved this. Alex's proof is the same as Darius' proof, but noting that $4\alpha n = 4\times\alpha n$ is four times the original number. James ignored the times table, which resulted in simpler notation:
Let $m =$ any multiple of a number. The differences of the squares of the numbers one digit above and one digit below this number can be represented, once again using algebra, as $$(m+1)^2 - (m-1)^2 = (m+2m+1) - (m-2m+1)$$ which equals $$m - -2m = 4m$$
Elissa used slightly different algebra, and included a diagrammatic proof as well as an algebraic proof:
$\begin{align}&(a+2)^2 - a^2\\
=&(a+2)(a+2) - a^2\\
=&a^2 + 4a + 4 - a^2\\
=&4a+4\hspace{5mm} = 4(a+1)\end{align}$
Diagrammatically:
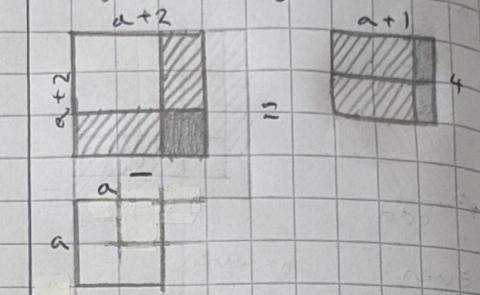
What about other gaps? Jonty from Long Field Academy, Sanika and Alex tried using gaps of 2 instead of 1. This is Alex's work:
$(x-2), x, (x+2)$
$\begin{align}(x+2) (x+2) &- ((x-2) (x-2))\\
=x^2 +2x+2x+4&-(x^2-2x-2x+4)\\
=8x \end{align}$
Jonty also tried using gaps of 3:
$(n+3)^2 - (n-3)^2 = n\times12$
I do believe there [are similar relationships for other numbers] as it works for all possibilities I've tried.
Amy from Long Field Academy and Daruis both proved some facts about any gap. This is Amy's work:
The formula to get the answer for this question is $4xn$, where $x$ is the number that you start with and $n=$ the amount that you count either side of that number.
The way that I got to this formula was by doing this equation:
$((x+n)\times(x+n)) - ((x-n)\times(x-n))$
This can be expanded out to:
$(x^2 + xn + xn + n^2) - (x ^2 - xn -xn -n^2)$
Which can be simplified to:
$2xn - -2xn$
When there are two subtraction signs next to each other, they would become an addition sign and so, you would get the answer $4xn.$
Darius, once again, noted that this is a multiple of $x$.
It is also possible to prove this result by factorising:
Suppose the two numbers are $a$ and $b$, where the number half-way between $a$ and $b$ is $n$, with $a = n+g$ and $b=n-g$ for some gap $g.$
$a^2 - b^2$ can be factorised as $(a+b)(a-b).$
$a+b$ is double the average of $a$ and $b,$ $\dfrac{a+b}{2},$ which is $n.$ So $a+b = 2n.$
$a-b$ is double the gap, because it is the distance from $b$ to $n$ plus the distance from $n$ to $a.$ So $a-b=2g.$
$\therefore a^2 - b^2 = (a+b)(a-b) = 2n\times2g = 4ng.$
Freya from Long Field Academy made a different observation by subtracting squares of consecutive numbers, rather than squares of numbers two apart. Click to see Freya's work.

Victor from KCLMS in the UK sent in a brave proof that the difference between two squares is always a multiple of three, regardless of whether they are near multiples of three. Here is Victor's work:
Claim: $a^2-b^2=3P$
(that is, taking the squares of any two integers $a$ and $b$, the difference will be $3P$ which is a multiple of three)
Proof:
$3K=a +10b$
($K$ is a name that Victor gives this number because it will be useful later in the proof)
$\Rightarrow 3K-10b=a$
$\begin{split}a^2-b^2&= (3K-10b)^2 -b^2\\
&=9K^2-60bK+100b^2 - b^2\\
&=9K^2-60kb+99b^2\\
&=3(3K^2 -20Kb +33b^2)\end{split}\\
\Rightarrow P= 3K^2 -20Kb +33b^2$
That looks very convincing, but we have seen from the examples above that it isn't always true! For example, $6^2-4^2 = 36-16 = 20,$ which is not a multiple of three. Can you spot the trick in Victor's proof? Click to see an explanation.
At the end of the proof, we end up with $P = 3K^2 - 20Kb + 11b^2.$ If $K$ is an integer then this will be an integer. However, if $K$ is not an integer, then $P$ might not be an integer either, so $3P$ might not be in the three times table. For example, when $b=4$ and $K=\frac{46}3,$ $P = 3K^2 - 20Kb + 11b^2 = \frac{20}3,$ and so $3P=20$ which is not in the three times table.
Teachers' Resources
This problem is available as a printable worksheet: Difference of Two Squares
Why do this problem?
This problem is an excellent context for observing, conjecturing and thinking about proof. It offers an opportunity for purposeful practice of algebraic manipulation of quadratic expressions.
Possible approach
"Choose any multiple of 3, take the numbers on either side of your chosen number, square them, and find the difference.
For example, if I chose 33, I would work out
$34^2=1156$
$32^2=1024,$
so the difference is $1156-1024=132$."
Collect some of the students' responses on the board.
"Is there anything special about all our answers?"
They are all multiples of 2.
They are all multiples of 3.
They are all multiples of 4.
They are all multiples of 12.
"With your partner, see if you can explain what you've noticed."
Give students some time to think about explanations, and circulate to listen to what they come up with. If no-one thinks of using algebra, pose the questions:
"Is there a way I can use algebra to represent a multiple of 3?"
"How can I use my algebraic representation to prove that the answer will always be a multiple of 12?"
Once students have engaged with the algebra, bring the class together once more and invite a couple of students out to the board to show their proofs.
Then set the follow-up challenge:
"What if we started with a multiple of 5 instead of a multiple of 3?" and invite them to explore and prove their cojectures in a similar way.
"Is there a similar relationship for other times tables?"
Possible support
Pair Products is a similar problem, but with a little more structure and support.
Possible extension
"What if we started with a multiple of $k$ instead of a multiple of $3$?"
