Reversals
Problem
Reversals printable worksheet
You may wish to try Always a Multiple? and Special Numbers before tackling this problem.
Where should you start, if you want to finish back where you started?
Alison chose a two-digit number, divided it by $2$, multiplied the answer by $9$, and then reversed the digits.
Her answer was the same as her original number!
Can you find the number she chose?
Then she chose another two-digit number, added $1$, divided the answer by $2$, and then reversed the digits.
Again, her answer was the same as her original number!
Can you find the number she chose this time?
Charlie chose a two-digit number, subtracted $2$, divided the answer by $2$, and then reversed the digits.
His answer was the same as his original number!
What was Charlie's number?
Choose a number, subtract $10$, divide by $2$ and reverse the digits.
What number should you start with so that you finish with your original number?
Extension
Choose a 3-digit number where the last two digits sum to the first (e.g. $615$).
Rotate the digits one place, so the first digit becomes the last (so for the example, we get $156$).
Subtract the smallest number from the largest and divide by $9$ (which is always possible).
What do you notice about the result? Can you explain why?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Student Solutions
Thank you to everyone who submitted solutions to this problem, and well done to all of you!
Many of you were able to find some or all of the reversals, including Brendon, from St Mary's Catholic High School; Harry, James and Lauren, all from Beccles Free School; and Ethan, Josh, Josh and David, from Danilack Middle School, Canada.
Amy, from Wheatley Park School, sent in this excellent explanation of how she was able to find the solution to the first problem:
Wayne and Jason, from ACS Barker, Singapore, explained how they found the answers for the other three parts:
Part 2
We found out that the number must be more than $21$, because $21-1=20$, and $20/2=10$, and if we try to reverse any number that is $10$ or less we will not get a two-digit number.
We found out that the number must be odd, as adding $1$ to odd numbers gives an even number and only even numbers give a whole number when divided by $2$.
We found out that the number cannot be $99$, $79$, $59$ and $39$ because adding $1$ to these numbers gives $100$, $80$, $60$ and $40$ and these numbers when divided by $2$ give $50$, $40$, $30$ and $20$ which cannot be reversed.
Within the narrowed range of numbers, we have:
- 23, 25, 27, 29
- 31, 33, 35, 37
- 41, 43, 45, 47, 49
- 51, 53, 55, 57
- 61, 63, 65, 67, 69
- 71, 73, 75, 77
- 81, 83, 85, 87, 89
- 91, 93, 95, 97
Part 3
We found out that the number must be more than $22$ because $22-2=20$ and when we divide $20$ by $2$, we would get $10$ and if we reverse a number that is $10$ or less, it does not give a two-digit number.
We found out the numbers must be even as subtracting $2$ gives an even number and only even numbers give a whole number when divided by $2$.
We found that the number cannot be $42$, $62$ or $82$, as when you subtract $2$ from them, divide the result by 2 and reverse the result, you will not get a double digit number.
Within the narrowed range of numbers, we have:
- 24, 26, 28
- 30, 32, 32, 34, 36, 38
- 40, 44, 46, 48
- 50, 52, 54, 56, 58
- 60, 64, 66, 68
- 70, 72, 74, 76, 78
- 80, 84, 86, 88
- 90, 92, 94, 96, 98
Part 4
We found that the number has to be even, as only even numbers$-10$ are divisible by $2$.
We found that the number must be above $30$ as $30-10=20$, $20 \div 2=10$ and numbers less than $10$ do not have a 2-digit reverse.
We found that the number must not be $50$, $70$, $90$ as these numbers minus $10$ and divided by $2$ give $20$, $30$ and $40$, which cannot be reversed
So we start narrowing down with this range of numbers:
- 32, 34, 36, 38
- 40, 42, 44, 46, 48
- 52, 54, 56, 58
- 60, 62, 64, 66, 68
- 72, 74, 76, 78
- 80, 82, 84, 86, 88
- 92, 94, 96, 98
Rachel, from NCLS Jeju in South Korea, used algebra to help her to find the solution to part 1:
If the two digit number has digits $ab$, then it can be written as $10a+b$.
Dividing by $2$ gives $\tfrac{10}{2}a+\tfrac{1}{2}b = 5a+\tfrac{1}{2}b$.
Multiplying by $9$ gives $45a + \tfrac{9}{2}b$
Since the answer is $10a+b$, when you return to the stage before reversing the digits, it becomes $10b + a$.
Since this is the same point as just after multiplying by $9$:
Simplifying this equation, it becomes:
$90a + 9b = 20b + 2a$ (multiplying by $2$)
$88a = 11b$
$8a = b$
Since $0 < a < 10$ and $0 \leq b < 10$, the only possible values of $a$ and $b$ are $a=1$ and $b=8$.
Therefore, the original number was $18$.
Sherry, also from NCLS Jeju, had this explanation for part 2:
Suppose the two-digit number is $ab$, so that it is equal to $10a+b$. When the number is reversed, it is $ba$, and is equal to $10b+a$.
From the given information, we can write the following formulae:
Then, since $8a$ is an even number, $8a+1$ is an odd number, so $19b$ is odd, and therefore $b$ is odd.
As $a \leq 9$, $19b=8a+1\leq 73$, so $b \leq 3\tfrac{16}{19}$.
Therefore the possible values for $b$ are $1$ and $3$.
If $b=1$, $19b=19$, so $8a=18$, which is not a multiple of $8$, so $b\neq 1$.
If $b=3$, $19b=57$, so $8a=56$ and $a=7$.
This means the starting number was $73$.
Zach solved parts 3 and 4 in a similar manner:
Part 3
From the question, if the number is $10a+b$, then:
$\frac{(10a+b)-10}{2}=10b+a$
Multiplying by $2$ gives: $10a+b-2=20b+2a$
Simplifying then gives $8a-2=19b$, so $a=5$ and $b=2$.
Since $\tfrac{1}{2}(52-2)=25$, this confirms that the number Charlie thought of was $52$.
Part 4
The initial number is $10a+b$. The question then says that $\tfrac{1}{2}((10a+b)-10)=10b+a$.
Multiplying by $2$ gives: $10a+b-10=20b+2a$
Simplifying then gives $8a-10=19b$, so $a=6$ and $b=2$.
Since $\tfrac{1}{2}(62-2)=26$, this confirms that the number Charlie thought of was $62$.
Julian, from the Britsh School, Manila, in the Philippines, used the programming language scratch to find the solutions. You can see his programs here:
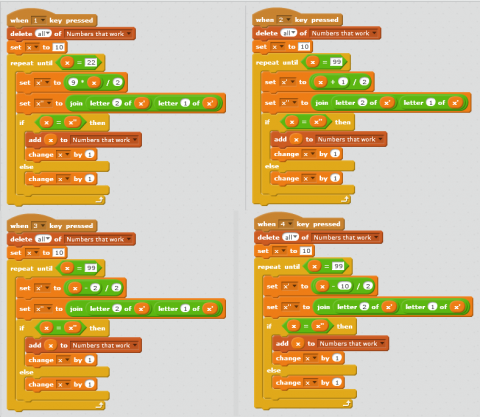
Both Zach and Julian were also able to solve the extension. Here is Julian's solution:
The answer will always be the last two digits of the original number reversed.
Let the second and third digits of the original number be $a$ and $b$ respectively.
The original number is $100(a+b)+10a+b = 110a+101b$
When you rotate the digits one place you get: $100a+10b+(a+b)$ = $101a+11b$
$(110a+101b)-(101a+11b)=9a+90b = 9(a+10b)$
Dividing by 9 we get $a+10b$
But the last two digits of the original number is $10a+b$!
So when you reverse the digits, you get $10b+a$.
Therefore doing this process is the same as reversing the last two digits of the original number.
Teachers' Resources
Why do this problem?
This problem strengthens students' understanding of place value and can help them to appreciate the power of algebra for solving number problems.
Possible approach
You may wish to work on the problems Always a Multiple and Special Numbers first.
Introduce the first problem:
"I chose a two-digit number, divided it by 2, multiplied the answer by 9, and then reversed the digits. My answer was the same as my original number. Can you work out what my number was?"
Give students time to think about the problem and discuss it with their neighbour. Then share approaches. If no-one has used algebra, introduce the idea of representing a two-digit number as 10a + b.
Next, give students the other three problems:
- I chose a two-digit number, added 1, divided the answer by 2, and then reversed the digits. My answer was the same as my original number! Can you find the number I chose?
- I chose a two-digit number, subtracted 2, divided the answer by 2, and then reversed the digits. My answer was the same as my original number! What was my number?
- Choose a number, subtract 10, divide by 2 and reverse the digits. What number should you start with to get an answer the same as your original number?
Possible extension
Choose a 3-digit number where the last two digits sum to the first (e.g. 615).
Rotate the digits one place, so the first digit becomes the last (so for the example, we get 156).
Subtract the smallest number from the largest and divide by 9 (which is always possible).
What do you notice about the result? Can you explain why?
These problems can all be solved using similar techniques:
Think of Two Numbers
Legs Eleven
Puzzling Place Value
Possible support
Always a Multiple provides a geometric as well as an algebraic way of thinking about place value related number puzzles, and might be a useful introduction to the ideas used in this problem.