Move Those Halves
For this task, you'll need an A4 sheet and two A5 transparent sheets. Decide on a way of arranging the A5 sheets on top of the A4 sheet and explore ...
Problem
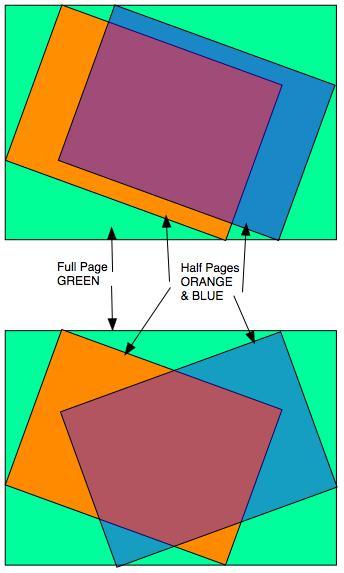
Explore where you can put these two halves and look at the overlap and the uncovered green parts.
There are no particular rules, it's just a matter of having an A4 sheet and the two transparent A5 sheets.
What different shapes and areas can you discover?
Teachers' Resources
Why do this problem?
This activity was initially developed for Wild Maths, our sister site, to encourage learners to be creative mathematicians. Mathematics is certainly a creative subject. It involves spotting patterns, making connections, finding new ways of looking at things and using what you already know in new contexts. Creative mathematicians play around with examples, draw pictures, have the courage to experiment and ask good questions. (Wild Maths is aimed at individual learners, rather than teachers so the notes below only appear on NRICH.)
Possible approach
How you approach this depends so much on the experience, knowledge and skills of your pupils. You could focus on designs, patterns, decribing shapes, fractions, area and making conjectures, for example.
Key questions
Tell me about your way of arranging the two halves.
What are you counting?
What do you notice?
What do you think you might do next?
Possible extension
Use quarters within the halves within the whole.
Possible support
Some pupils may need physical help if their fine motor skills will not allow them to do what they are trying to do.
