Quadratic Patterns
Surprising numerical patterns can be explained using algebra and diagrams...
Problem
Quadratic Patterns printable worksheet
Charlie has been playing with calculations again...
$2 \times 4 + 1 = 9$
$4 \times 6 + 1 = 25$
$5 \times 7 + 1 = 36$
$9 \times 11 + 1 = 100$
What do you notice?
Click below to see what Charlie said:
"If you multiply two numbers that differ by 2, and then add one, the answer is always the square of the number between them!"
Can you explain what's happening?
Click below to see Charlie's explanation:
$ n(n+2) +1 = n^2 +2n+1 = (n+1)^2$
or alternatively,
$(n-1)(n+1)+1 = n^2-n+n-1+1=n^2$
Alison drew a diagram to explain the results. Click below to see:


Can you make sense of Charlie's method and Alison's diagrams?
Here are some more number patterns to explore. Some have been expressed numerically, some in words, and some algebraically.
Can you represent each pattern in all four ways,
numerically (so you can spot the pattern),
in words (so you can describe the pattern),
algebraically (so you can prove the pattern continues),
and using a diagram (to explain the pattern)?
- $2 \times 3 + 3 = \, ?$
$5 \times 6 + 6 = \, ?$
$4 \times 5 + 5 = \, ?$
$9 \times 10 + 10 = \, ?$
What do you notice?
- Choose three consecutive numbers, square the middle one, and subtract the product of the other two.
Repeat with some other sets of numbers.
What do you notice?
- $3 \times 3 - 1 \times 1 = \, ?$
$8 \times 8 - 6 \times 6 = \, ?$
$7 \times 7 - 5 \times 5 = \, ?$
$10 \times 10 - 8 \times 8 = \, ?$
What do you notice?
- $n(n+1) - (n-1)(n+2) = \, ?$
$(n+1)(n+2) - n(n+3) = \, ?$
$(n-3)(n-2) - (n-4)(n-1) = \, ?$
What do you notice?
- $3\times 5 + 1= \, ?$
$5\times 7 + 1= \, ?$
$7\times 9 + 1= \, ?$
$9\times 11 + 1= \, ?$
What do you notice?
- Choose three consecutive numbers and add the product of the smallest two to the product of the greatest two.
Repeat with some other sets of numbers.
What do you notice?
With thanks to Don Steward, whose ideas formed the basis of this problem.
You may be interested in the other problems in our Factorise This! Feature.
Getting Started
You could start by taking a look at Perimeter Expressions and Seven Squares, which offer a good introduction to describing patterns verbally, numerically and algebraically.
Student Solutions
We have received many excellent solutions for these problems. Well done to all of you who included numerical, diagrammatic and algebraic representations and descriptions in words for these problems. Particularly well done to Diana from Dulwich College Beijing in China, Sameera from Ripon Grammar School, Amrit from Hymers College, Chloe, Sophia and Shreya from North London Collegiate School, Maddy and Grace from the Stephen Perse Foundation and Peter from Durham Johnson School in the UK, Aarav, Ruhi, Sehar, Nikhil, Vishnuvardhan, Ahana, Ananthajith, Dhruv, Vihaan, Arya, Aaradhya and Vishnu from Ganit Kreeda, Vichar Vatika, India, Shaunak also from India, Miriam from IES Maximo Laguna and Marc and Yang from King's College Alicante in Spain, Radi and Camilla and Viktor and Matija from European School Varese in Italy, Ziqian from Harrow International School in Hong Kong, Rubayat, Hondfa, Jacob and Nathan from Greenacre Public School in Australia, and Ryan from Dulwich College Seoul in Korea.
1.
Amrit from Hymers College in the UK, Radi and Camilla and Viktor and Matija from European School Varese in Italy, Rubayat, Hondfa, Jacob and Nathan from Greenacre Public School in Australia, Ryan from Dulwich College Seoul in Korea and Peter from Durham Johnson School in the UK sent in good work on this problem.
Viktor and Matija spotted a numerical pattern and summarised it in words:
$2 \times 3 + 3 =9$
$5 \times 6 + 6 =36$
$4 \times 5 + 5 =25 $
$9 \times 10 + 10 =100$
If you multiply the two consecutive numbers, which differ by one, then add the bigger number to that you're always going to get the square of the bigger number.
Ryan showed numerically why this works:
$$\begin{align}2 \times 3 + 3 = 9 &= 3 + 3 + 3 = 3 \times 3 = 9\\
5 \times 6 + 6 = 36 &= 6 + 6 + 6 + 6 + 6 + 6 = 6 \times 6 = 36\\
4 \times 5 + 5 = 25 &= 5 + 5 + 5 + 5 + 5 = 5 \times 5 = 25\\
9 \times 10 + 10 = 100 &= 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10+ 10 = 10 \times 10 = 100\end{align}$$
Amrit, Sehar, Nikhil, Vishnuvardhan, Ahana, Ananthajith, Dhruv, Vihaan, Arya, Aaradhya and Vishnu gave algebraic proofs. This is Amrit's algebraic proof:
Represented algebraically, this is $n(n+1)+(n+1)$
Factorising, $(n+1)(n+1)$
And we see this is $(n+1)^2$
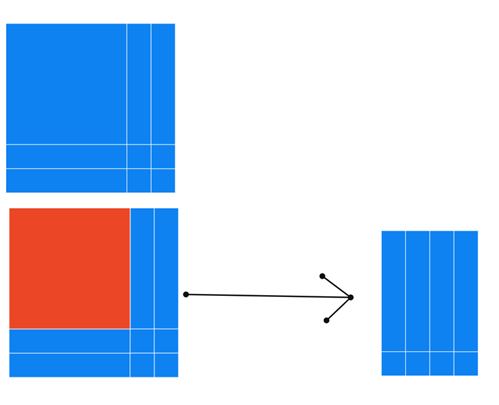
Sehar, Nikhil, Vishnuvardhan, Ahana, Ananthajith, Dhruv, Vihaan, Arya, Aaradhya and Vishnu combined algebra and words to explain this result:
$n(n+1)$ means $(n+1)$ added $n$ times.
$n(n+1)+n+1$ means $(n+1)$ added $(n+1)$ times.
So, $n(n+1) +n+1 = (n+1)(n+1)=(n+1)^2$.
They then represented this in a diagram. The rectangles with black sides show the left hand side of their equation and the red square shows the right hand side.

Radi and Camilla gave a diagram which represented the equation using similar ideas:
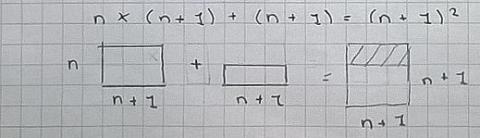
2.
This is Radi and Camilla's work for the second part of the problem:

Radi and Camilla used $a, a+1$ and $a+2$ to represent three consecutive numbers. Diana and Sameera used a slightly different algebraic representation. Here's Sameera's working. Can you see how this represents the three consecutive numbers?
$n^2-(n-1)(n+1)=n^2 - (n^2-1)= n^2-n^2+1=1$.
Sameera also sent in this image of her diagrams that explained the result. Unfortunately the picture is a bit blurred, but can you use her diagrams to work out what her explanation might be?

3.
Viktor and Matija spotted the numerical pattern for the third part of the problem:
$3\times3-1\times1=8$
$8\times8-6\times6=28$
$7\times7-5\times5=24$
$10\times10-8\times8=36$
Amrit put it in words:
If you take two numbers with a difference of 2 and subtract the square of the smaller one from the square of the bigger one, the result is four times the mean of the two numbers.
Aarav noticed something about how the values changed and put this into words:
I noticed that by each increasing pattern the answer of equation increases by 4.
Can you connect these two ways of describing the pattern with the other representations?
Tiago and Finn and Shaunak proved it algebraically. Here's Tiago and Finn's proof:
$$\begin{align}(n\times n)-(n-2)\times(n-2)=&n^2-(n-2)\times(n-2)\\
=&n^2-(n^2-4n+4)\\
=&n^2-n^2+4n-4\\
=&4(n-1)\end{align} $$
Shaunak used $n$ and $n+2$ as her two numbers that differ by 2, which gave a slightly different algebraic argument:
$(n+2)^2-n^2=n^2+4n+4-n^2=4n+4=4(n+1)$.
Peter thought about it differently:
The answer is always the sum of the digits [multiplied by 2]. $a\times a-b\times b=2b+2a$ if $a-b=2$.
Marc and Yang called the numbers $x$ and $y$ and noticed that
$x^2 - y^2 = (x+y)(x-y)$
Amrit's proof used Marc and Yang's idea to prove Peter's representation in words.
$(x+2)^2-x^2=(x+2+x)(x+2-x)$, which simplifies to $(2x+2)(2)$
Tiago and Finn's diagram representation looked like this:
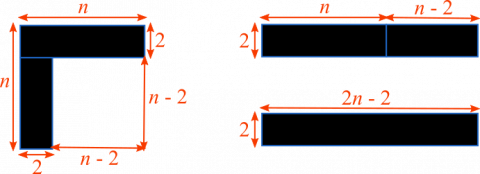
Like her algebra, Shaunak's diagram was slightly different. Can you relate the diagram to Shaunak's algbera and connect her argument with Tiago and Finn's diagram?
4.
Peter from Durham Johnson School in the UK noticed that the expressions all simplify to 2:
$n(n+1)-(n-1)(n+2)=2$
$(n+1)(n+2)-n(n+3)=2$
$(n-3)(n-2)-(n-4)(n-1)=2$
The following observations can be made:
"If you choose four consecutive numbers and subtract from the product of the two middle ones the product of the other two, then you always get $2$."
General expression: $n(n+1) - (n-1)(n+2) = (n^2 + n) - (n^2 + n - 2) = 2$.
It follows that $(n+1)(n+2) - n(n+3)$ and $(n-3)(n-2)-(n-4)(n-1)$ are always $2$.
These diagrams represent the process. The shaded area in the right hand diagram needs to be 'subtracted' from the green area.

This leaves a gap of 2 squares:

5.
Maddy and Grace from the Stephen Perse Foundation in the UK continued the numerical pattern:
$2 \times 4 + 1 = 9$
$4 \times 6 + 1 = 25$
$5 \times 7 + 1 = 36$
$9 \times11 + 1 = 100$
$10 \times 12 + 1 = 121$
$20 \times 22 + 1 = 441$
Rubayat, Hondfa, Jacob and Nathan from Greenacre Public School in Australia noticed that
The pattern is what Charlie quoted,"If you multiply two numbers that differ by 2, and then add one, the answer is always the square of the number between them!" $3 \times 5 + 1= 16$ or $4^2$. $5 \times 7 + 1 =36$ or $6^2$.
Peter's proof was different to Charlie's:
$(n-1)(n+1)= n^2-1$, so $(n-1)(n+1)+1=n^2$
Chloe, Sophia and Shreya from North London Collegiate School made a clear diagram with a good explanation:
Ziqian included a similar diagram, but explained the result as a rearrangement of the pieces:
In the diagram we can also see that by moving the pieces and adding 1 we get the number we started from $=x^2$.
6.
Rubayat, Hondfa, Jacob and Nathan represented the problem numerically and in words:
The result equals the middle number squared, then times by $2$. For example: $1,2,3.$ $1 \times 2=2,$ $2 \times 3=6$ therefore $6 +2 = 8$ [which is $2^2$ times $2$].
Another example is $50,51$ and $52.$ $50 \times 51= 2550,$ $51 \times 52= 2652.$ Therefore
$2550 + 2652=5202.$ $51$ squared then times $2$ equals $5202.$
Amrit proved it algebraically:
Represented algebraically, this is
$$x(x+1)+(x+1)(x+2)$$Factorising,$$(x+1)(x+x+2)$$Simplifying,$$(x+1)(2x+2)$$Factorising,$$2(x+1)(x+1)$$Simplifying,$$2(x+1)^2$$
Clare made a diagram:

Sehar, Nikhil, Vishnuvardhan, Ahana, Ananthajith, Dhruv, Vihaan, Arya, Aaradhya and Vishnu used a similar diagram, but like Sameera, they had used $n-1, n$ and $n+1$ as their three consecutive numbers so their diagram is slightly different:

We had so many good solutions to this problem. Well done again to everyone who submitted solutions!
Teachers' Resources
This problem is available as a printable worksheet: Quadratic Patterns
Why do this problem?
This problem offers students the opportunity to engage with quadratic number patterns using multiple representations - in words, numerically, algebraically, and with diagrams.
By moving between different representations for different purposes, students gain a deeper understanding of the underlying structure of quadratic sequences.
Possible approach
Write up Charlie's four calculations on the board:
$2 \times 4 + 1 = 9$
$4 \times 6 + 1 = 25$
$5 \times 7 + 1 = 36$
$9 \times 11 + 1 = 100$
"Here are four calculations. Take a moment to look at them and see what you notice."
"Now share your ideas with your partner."
Invite a few pairs to describe what they noticed -
Charlie always added 1,
the answer was always a square number...
"It looks as though if you multiply two numbers that differ by 2, and then add one, the answer is always the square of the number between them!
I wonder if we can prove that it will always work?"
Give students some time in pairs or small groups to explore and think of ways of convincing themselves that the pattern continues. While they are working, circulate and listen to the ideas they come up with.
In particular, look out for students explaining the pattern algebraically or with a diagram, like Charlie and Alison did in the problem.
After a while, bring the class together and invite any students with an algebraic or diagrammatic way of explaining the pattern to come out to the board and share their method, or if no-one used Charlie's or Alison's method, show it to them.
Once students are comfortable with the different representations, they could work through the problems on this worksheet, proving their findings with algebra and a diagram each time.
Key questions
How can we represent the patterns algebraically?
How can we interpret the product of two numbers geometrically?
Possible support
Perimeter Expressions and Seven Squares offer students a good introduction to describing generic patterns verbally, numerically and algebraically.
Possible extension
Pair Products and Hollow Squares offer more opportunities for observing, conjecturing and thinking about proof in the context of quadratic relationships.
