Homes

Six new homes are being built! They can be detached, semi-detached or terraced houses. How many different combinations of these can you find?

Number Squares

Start with four numbers at the corners of a square and put the total of two corners in the middle of that side. Keep going... Can you estimate what the size of the last four numbers will be?

I'm Eight

Find a great variety of ways of asking questions which make 8.

Routes 1 and 5

Age 5 to 7
Challenge Level

Fiona from Tattingstone School tackled this very clearly:

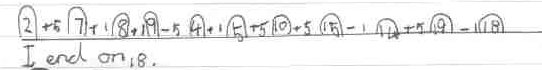
She found another way of starting and ending on these numbers:

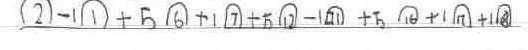
Fiona then explains:

Omar from the Modern English School, Cairo drew out a few different routes which also start at $2$ and end at $18$:

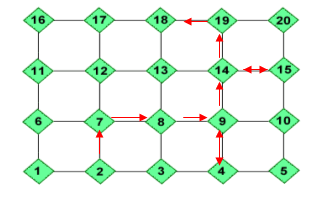
I like the way you've shown the 'optional extras' with double-headed arrows, Omar Abdel also from the Modern English School found another route:

$2+1+1+5-5+1+5+5-1+5-1$

Elliot, Richard and Christopher from Moorfield Junior School agreed with Fiona but also found another equally short route: $+1,+5,+5,+5$.

Molly and Callum from Bradon Forest School sent us a detailed response:

The last number in the sequence is $18$, and another Sequence is $2(+5)7(+5)12(+5)17(+1)18$.

But the last one is the hardest. Still using the example $2$-$18$ above you need to subtract the biggest number from the smallest one ($18-2=16$)

The number you are left with is the number that all the steps shold add up to, or 'special number' ($5+5+5+1=16$) or ($5+1+1-5+1+5+5-1+5-1=16$) To find out the number of steps and what they are add keep adding together $5$'s until you reach the number closest to the special number ($3\times5=15$ is closer to $16$ than $4\times5=20$). Then continue adding or subtracting $1$'s until you get the special number ($15+(1\times1)=16$). This might be a bit clearer;

$3\times5 = 15$

$1\times1 = 01$ = $16$ --special number in four steps

You can try that on any sequence and it'll still work!!!

Luke from Witton Middle School noticed something important:

For the first part of the challenge, I worked out that the number you ended on was $1$8.

So for the second part of the challenge, I did:

$2 +1 (3) +5 (8) -1 (7) +5 (12) -1 (11) +5 (16) +1 (17) -5 (12) +1 (13) +5 =18$

Then I used cancelling down (for example, $+1$ and $-1$ can be cancelled out because whatever number is the input, the output will be the same as the input. e.g. $32 +1 -1 =32$).

To end up with the shortest route - $2 +5 +5 +5 +1 =18$.

You could add in a different order but the answer would be the same.

Well done, Luke, you're right that the order of the operations is not important - you would still get to $18$.

You may also like

Homes

Number Squares

I'm Eight

Routes 1 and 5

Age 5 to 7Challenge Level

Age 5 to 7
Challenge Level