Home time
Problem
Alice, Beccy, Craig, David, Ellie and Francis all go to the same school. Usually they catch the bus home, but today they are staying later for hockey club. Alice lives the closest to school, so they walk round there and her mum gives the others a lift home.
The map below shows how the children's houses are connected by road (it is not to scale!). To make things easier, just the first letter of each name has been used.
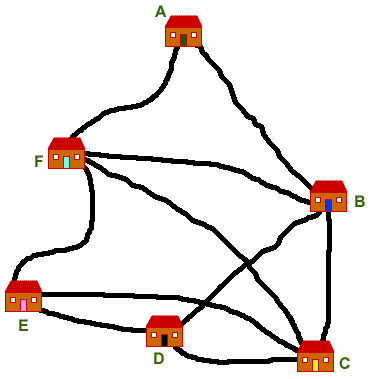
Alice's mum sets off from their house (A) with all the children. She needs to go to each house just once and then back home again. How many different routes are there?
In the end, she took a route like this:
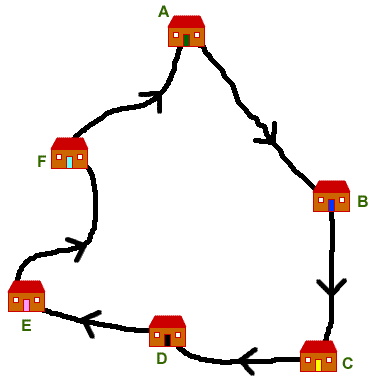
The entire journey took $1\frac{1}{2}$ hours and she was travelling at an average speed of $30$ miles per hour.
The total distance from A to D is the same as the total distance from E to A, which is $19$ miles.
It took twice as long to get from B to D as it did from D to E.
A is twice as far from F as it is from B.
The distance between A and B is a third of the distance between C and E.
Using this information can you find out how long each road is on the route taken by Alice's mum?
Getting Started
Knowing how long the journey took and the speed she travelled means you can work out the total distance they went.
Using this and the second piece of information, how far is it between D and E?
Student Solutions
Sean at Great Clacton Junior School worked out there were six routes for Alice's mum to take.
Three children from Tattingstone School tackled this problem.
Sarah drew the routes out which makes it very easy to see:

Marion re-labelled the roads like this:

Then she explained how she worked out the distances:

Georgia did it a very similar way:

All very well explained - well done!
Sam from Newberries Primary School also discovered the answer working in a similar way.
