Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Networks and Nodes
Age 7 to 11
Challenge Level 





 |
 |
 |
 |
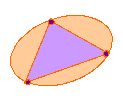
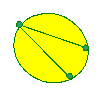
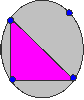
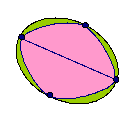
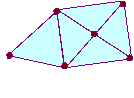
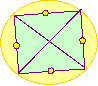
Without taking your pencil off the paper or going over a line
or passing through one of the points twice, can you follow each of
the networks?
If you are able to do this, mark your pathway and direction using arrows. Create your own networks. Can you draw one that is impossible to complete without lifting your pencil? |
 |
 |
 |
 |

