A flying holiday
Problem

A bird flew north for $20$ minutes, north-west for $50$ minutes, then south for $20$ minutes.
The bird keeps flying at about the same speed.
For how long, and in what direction, would the bird have to fly to return to its starting point?
Getting Started
What sort of picture might help you record the time and the direction?
The bird flies at the same speed all the time. That means the distance it travels north is the same as the distance it travels south. Does that help?
Student Solutions
We received a lot of responses to this problem - thank you to everyone who got in touch. Abdurraheem from Malmesbury Primary said:
North and south are opposites, AND they flew in those directions for the same amount of time, so they don't matter.So all that's left is north-west for $50$ minutes.
The opposite of north-west is south-east, and the amount of minutes must be the same, so the answer is: South-east for $50$ minutes.
You have thought very logically here, Abdurraheem. Well done.
Many of you drew the route that the bird takes, which is a very efficient way of solving the problem. Someone who didn't give their name or school sent in this image which is very helpful:
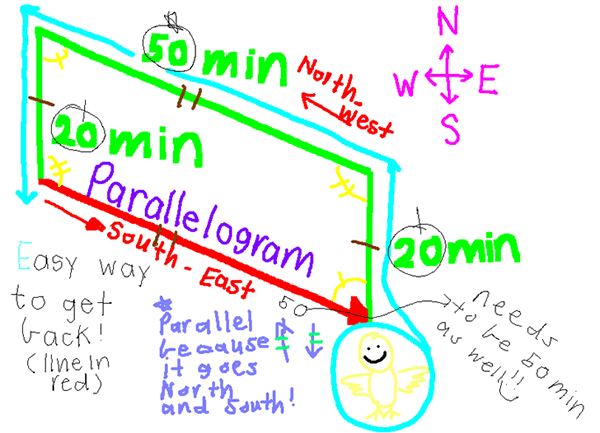
Christina, Amy and Keira from Dr Challenor's High School did the same thing and explained their reasoning:
South east for $50$ minutes.This is because the shape that all his travels need to make is a parallelogram. Any two opposite sides of a parallelogram are equal. So therefore north west is opposite to south east and $50$ is equal to $50$.
Joshua and James from Thornton Dale C of E Primary School used a similar method but they decided to draw the route to scale rather than sketch it. They describe what they did:
We drew out the bird course with $20$ minutes being $2$cm and $50$ minutes being $5$cm. Also we drew a compass showing north, north-east, east, south-east, south, south-west, west and north-west. After plotting the course we worked out which direction it was back to the beginning and measured the gap and put it into minutes.Daniel from Mount Pleasant Junior School described what he did very succinctly:
The answer is south east for fifty minutes. Here's how I did it:1.) I drew the map with the scale being ten minutes per cm. It looked like a parallelogram without the bottom side.
2.) I drew the shortest line from the destination to the start and it was $5$ cm south east meaning the time taken was fifty minutes.
Children from the Challenge Club at Pipers Corner School wrote to say:
We thought of two solutions:1. The bird could turn around and fly back the way it came.So it would fly $20$ mins North, $50$ mins South East and $20$ mins South (total $90$ minutes)
2. The bird would fly $50$ mins South East. Its route forms a parallelogram.
Well done! I guess the problem didn't actually ask for the shortest way back so you're right, the bird could have gone back the way it came. In fact, there could, therefore, be many, many other solutions!
Teachers' Resources
Why do this problem?
This problem is short and suitable for an introductory activity on representing and recording journeys, which is often problematic. It brings together the idea of direction through compass points, and the more difficult idea of constant speed.
Possible approach
Then give out the problem and suggest that the children act it out in pairs before recording it on grid paper.
Key questions
What sort of drawing might help?
Possible extension
Possible support
Some children will find the speed/distance complexity difficult. Reword the question as: A bird flew north for $20$ km, north-west for $50$ km, then south for $20$ km. How far, and in what direction would the bird have to fly to return to its starting point?
