Build It Up
Can you find all the ways to get 15 at the top of this triangle of numbers? Many opportunities to work in different ways.
Problem
We start with any four numbers (not zero!):
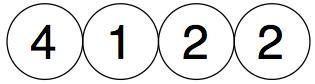
We then add them in pairs and place the total above them:
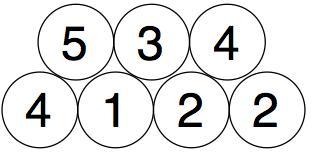
And we then add in pairs the new numbers we just got:
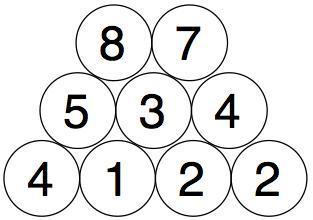
We do the same with those two numbers to get our final number:

You need to find four starting numbers to place at the bottom so that the top number will be 15.
Try to find as many sets of four starting numbers as you can.
Think about good ways to do this. Maybe use a system!
What little change can you make to the rules to explore again?
What new ideas can you think of to make this different? Explore those!
You may like to take a look at the follow-on activity Build it up More.
Student Solutions
We had a very large number of solutions come in for this challenge. Here are a selection for you to consider.
Primary 6 at Victoria Primary School in Scotland sent in this very thorough solution
Firstly, we looked at the 4 numbers at the bottom and tried to work out how to get to 15. As a class we agreed that this would take too long for us to try and work out all the 4 digit numbers. So next we worked out a system...
We started at the top and worked out all the 2 digit numbers that make 15 which were
14 + 1; 13 + 2; 12 + 3; 11 + 4; 10 + 5; 9 + 6; 8 + 7; 7 + 8; 6 + 9; 5 + 10; 4 + 11; 3 + 12; 1+ 14;
Then we looked at next row down and worked out that we couldn't have 1 + 14 and 14 + 1 because we we couldn't use 0 so nothing adds up to 0. We took a pair of numbers each and worked out some of the group of 3 numbers which were:
| making 15 | making | the | two | totals | |||
| 9 + 6 | 8,1,5 | 7,2,3 | 6,3,2 | 5,4,3 | 4,5,1 | ||
| 5 + 10 | 4,1,9 | 3,2,8 | 2,3,7 | 1,4,6 | |||
| 12 + 3 | 11,1,2 | 10,2,1 | |||||
| 6 + 9 | 3,3,6 | 2,4,5 | 1,5,4 | 4,2,7 | |||
| 11 + 4 | 10,1,3 | 9,2,2, | 8,3,1 | ||||
| 8 + 7 | 7,1,6 | 6,2,5 | 5,3,4 | 4,4,3 | 3,5,2 | 2,6,1 | |
| 7 + 8 | 3,4,5 | 5,2,6 | 6,1,7 | ||||
| 10 + 5 | 9,1,4 | 8,2,3 | 7,3,2 | 6,4,1 | |||
| 3 + 12 | 1,2,10 | 2,1,11 | |||||
| 13 + 2 | 12,1,1 | ||||||
| 4 + 11 | 3,1,10 | 2,2,9 | 1,3,8 |
And from that we were able to do the exact same to work out the four
numbers which are:
2221; 8111; 4122; 4211; 5212; 3211; 5211; 4122; 7112; 5114; 3213; 3123; 7112; 2131; 7112; 7223; 5211; 2214; 2311; 8231; 1312; 6113; 1127; 1118; 4212;
We really enjoyed the challenge and our (something? brains? hands? minds ?) hurts after it but in a good way.
We really needed to keep a growth mindset.
This has been explained very well but now have a look at the ones I've put in italics (and underlined) what do you think about them?
We also had a number of solutions sent in from Peak School in Hong Kong
Alyssa wrote:
I found that all of my solutions always had a 1 in the bottom row, and the
total of all the numbers in the bottom row was always an odd number.
Victoria K & F wrote:
These are our solutions:

Rules:
There has to always be a 1 in the bottom row.
In the bottom row will always be a number repeated twice.
The bottom row must equal an odd number.
The second to bottom row must equal 11, 12 or 13.
There must be a combination of odd and even numbers in every row.
Mathias wrote:
I found out 9 different ways to get 15 using different numbers.

Sophie and Dorika wrote:
We think that the bottom line has to add up to an odd number.
We also found out that there has to be a one in in the bottom row.
The middle line can't have a one in it.
The second to bottom row will equal to 11, 12, 13.
On the bottom row a number will always be repeated twice or three times.
There are only 4 pairs of numbers that can be used in the second row.

Extension:
We combined your idea and we did our own version using decimal points
15
9 6
6 3 3
4 2 1 2
2.5 1.5 .5 .5 1.5
1.25 1.25 .25 .25 .25 1.25
.125 1.125 .125 .125 .125 .125 1.125
Chloé, Holly and Anna wrote:
We found these solutions by starting from the top row and working our way
to the bottom:

We found some rules after finding the solutions:
-The bottom row must equal an odd number (7, 9, 11)
-The second to bottom row equal 11,12 or 13
-On the bottom row there will always be a number repeated twice
-There has to be be one in the bottom row
Thanks for reading!
Jihun from Dong Sung Elementary School in South Korea sent in the workthat had been done:
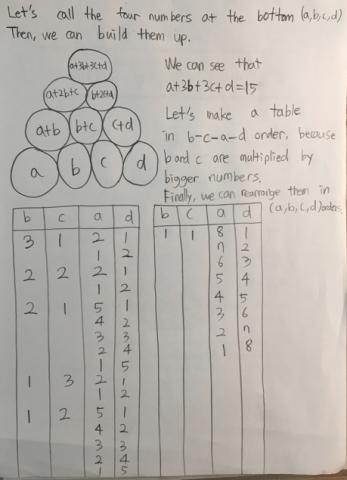
Well done all of you. It was very interesting reading about your methods and the things that you found out that had to be. Keep up your good work.
Teachers' Resources
Why do this problem?
This activity was initially developed for Wild Maths, our sister site, to encourage learners to be creative mathematicians. Mathematics is certainly a creative subject. It involves spotting patterns, making connections, finding new ways of looking at things and using what you already know in new contexts. Creative mathematicians play around with examples, draw pictures, have the courage to experiment and ask good questions. (Wild Maths is aimed at individual learners, rather than teachers, so the notes below only appear on NRICH.)
Possible approach
When the simple rules have been outlined and the example worked through some pupils may be happy recording their trials on paper. Some children might like to have little circles of paper/plastic/wood that they can write numbers on and so place them accordingly.
When a number of solutions have been found some good discussions may be had with the pupils sharing their observations as to what they notice and what does not work.
Key questions
Tell me about what's happening with the ideas you've tried.
Tell me about what's happening here (where they are at at the moment)
Possible extension
One way of extending this task is to start with more numbers at the bottom. For example, children could start with a triangle with these seven numbers at the bottom: 1, 2, 4, 8, 16, 32 and 64. These numbers can be added in the same way and pupils can see what they notice about the numbers they find at each level of the triangle. Some children might enjoy having a go at Build it Up More which is a 3D version of the challenge.
Possible support
If some pupils need help with keeping a record of what they've done, some adult support may be required.
