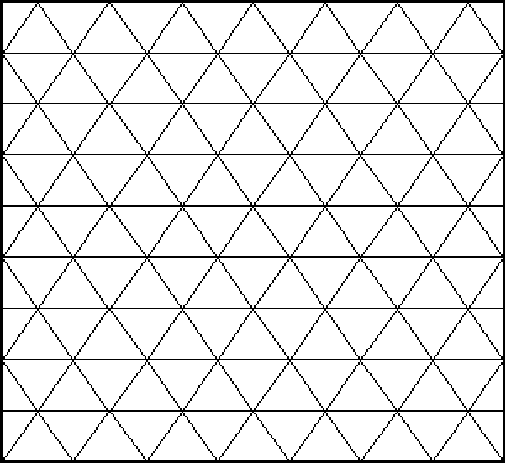
Where Are They?
Use the isometric grid paper to find the different polygons.
Problem
Use the isometric grid paper or the interactivity below to find the following polygons:
- A rectangle
- A rhombus
- A trapezium
- A parallelogram that is not a rectangle
- An equilateral triangle
- A right angled triangle
- A scalene triangle
- An isosceles triangle that is not an equilateral triangle
- A pentagon
- A hexagon
- A heptagon
- An octagon

Getting Started
If you're having trouble finding some of the shapes, you could print off this sheet.
Student Solutions
The pupils from Moorfield Juniors in Stockport sent in many solutions to this problem. Well done to each of you. The first piece of work was received from Steven and Matthew, who sent along the following shapes that they were able to find and recognise on the isometric paper.
Many other shapes were found by Moorfield's pupils, some of them were irregular and some were even difficult to put a name to! They certainly demonstrated their powers of observation.
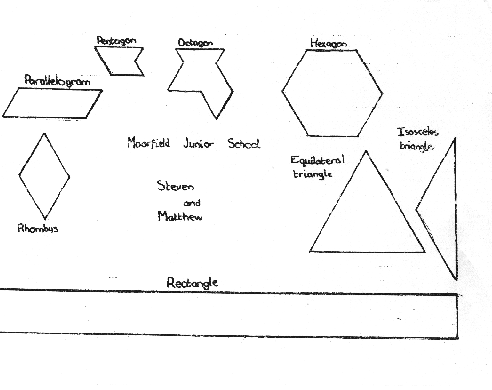
Can you find any other examples of the shapes that were named?
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support