What's It Worth?
There are lots of different methods to find out what the shapes are worth - how many can you find?
Problem
What's it Worth? printable worksheet
Each symbol has a numerical value. The total for the symbols is written at the end of each row and column.
Can you find the missing total that should go where the question mark has been put?
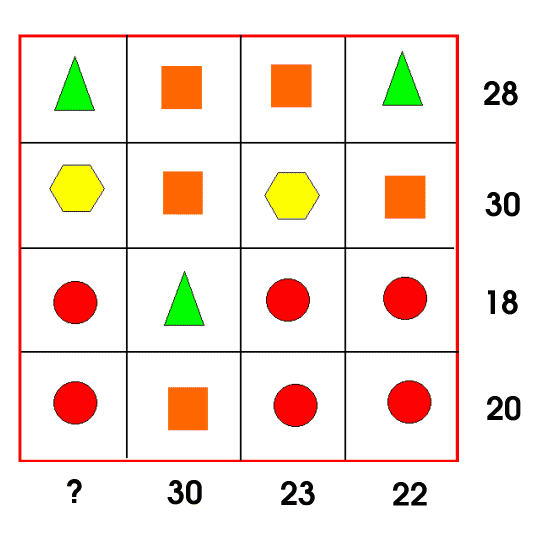
Image description
For accessibility: A 4 by 4 grid of triangles T, squares S, hexagons H, and circles C.
From left to right, top to bottom, the grid reads: T, S, S, T; H, S, H, S; C, T, C, C; C, S, C, C.
The totals for the rows from top to bottom are: 28, 30, 18, 20.
The totals for the columns from left to right are: ?, 30, 23, 22.
There's a lot of information in the grid, so you will need to make some choices about what to focus on first. Click below to see some images that draw your attention to particular parts of the grid.
What can you deduce from each image?
Can you find any other ways of solving the problem?
You can apply these strategies to similar problems.
Fruity Totals can be used to generate lots of different examples.
Getting Started
What can you deduce by comparing the bottom two rows?
If you could work out the value of the square, how could you then work out the value of the triangle?
Student Solutions
Well done to everybody who sent in a completed grid, or found the value of ?
Click to see methods using each of the images suggested, or read below to see the other methods we were sent.
Image 1
Eve, Karan and Maya from Tanglin Trust School (TTS) in Singapore, Joseph and Jeremy from Comet Bay College in Australia, Evie from Channing in the UK and Prinn and Utkarsh from Bangkok Patana School in Thailand all began with this reasoning described by Eve:
If you look at the second column you can see there are three squares and one triangle and if you look at the first row you can see it is the same but with two triangles and two squares. The total of the column is 30 but the total of the row is only 28, this means that the square must be worth two more points than the triangle.
Most people used trial from here, or 'worked out' the numbers, but Evie used a method which would also work for larger numbers:
Then you take away 4 ( = 2 points for each of the 2 squares) from 28 so that we can pretend all the numbers on the row are equal. If you divide 24 (28$-$4) by four, you have 6. You then have a strong suspicion that the triangle is 6 and the square is 8. If you try out your theory on the second line that goes down,you prove your theory right.
They then used 6 and 8 for the triangle and square to find which numbers the other shapes represent, and that ? = 21
Image 2
Krista from Bangkok Patana School in Thailand wrote:
Let's say the top row is 'row A' and the side row is 'row B'
Step 1
If we take a look at Row A, you can see that it consists of two triangles, two squares and the total is 28; therefore, we can give the equation of Row A as
2 triangle + 2 square = 28
Step 2
If we simplify the equation, we get triangle + square = 14
Step 3
Now take a look at Row B, we can see that it consists of a triangle, a square, 2 circles and the total is 22. Since we know that a triangle + square = 14 we can subtract [14 from] 22 to find out the sum of 2 circles: (22 - 14) = 2 circles = 8; therefore, 1 circle = 4
Image 3
Tuna, Jenny, Dana, Kayne, Angel & Tiger from Bangkok Patana School in Thailand wrote:
Step 1: Firstly, ignore the top row as well as the circles since it is not important at this stage.
Step 2: Look at the difference between the two numbers as well as the shapes. The difference between the triangle and the square is two as the difference between the numbers is two.
Step 3: After that, you just look at the top row and do trial and error
(or a method like Evie's described in Image 1)
Step 4: After you find all of the shapes' values you can add all of the values together and find the value of the question mark.
Image 4
We received methods starting from the bottom two rows which mainly used trial and improvement, so they are shown below as trial methods.
Here is a logical method using this image:



Four circles are 16 so circles are 4 each
Use the bottom two rows to find the value of the triangle and the square, and continue
Image 5
Palak and Armaan from Bangkok Patana School in Thailand wrote:
We know that 3 circles and one square adds up to 20 and 3 circles and a triangle adds up to 18. We can tell that the difference between the square and the triangle is 2 because 3 circles have to equal the same amount.
From there, they found the value of each shape. Here is a quicker method:
The first column contains 2 circles, a hexagon and a triangle, and the third column contains 2 circles, a hexagon and a square. So the third column adds up to 2 more than the first column, since the square is worth 2 more than the triangle.
So ? = 23 $-$ 2 = 21
Image 6
Van Anh from British Vietnamese Internation School Hanoi, Tejaswini and Mohinika and Misha from North London Collegiate Junior in the UK, Oliver from Tanglin Trust School in Singapore, Mikaeel from the UK and Shihyun and Junwoo from Bangkok Patana School in Thailand used this image. Mikaeel wrote:
Consider a grid of 16 numbers arranged in 4 by 4 grid. If we were asked to find the sum of the all the numbers we could:
a) find sum of each of the row, then find the total of the sums of each row, or
b) find the sum of each column, then find the total of the sums of each column.
To find the sum of all the numbers in the grid (for this problem) we could either find the sum of the rows, or find the sum of the columns. Therefore, the total of all the numbers in the grid is
28 + 30 + 18 + 20 or ? + 30 + 23 + 22.
This means that:
28 + 30 + 18 + 20 = ? + 30 + 23 + 22
96 = ? + 75
21 = ?
Thus, the missing total is 21.
Many solutions included a lot of 'educated guessing' or 'trial and improvement'. This method from Prim, from Bangkok Patana School in Thailand, shows a systematic trial approach:

Philip from Abingdon School in the UK came up with this neat solution:

If the top row is worth 28 and has 2 squares and 2 triangles and the second row is worth 30 and has 2 squares and 2 hexagons, we can deduce that 2 hexagons are worth 2 less than 2 triangles, or that a triangle is 1 less than a hexagon.

By repeating this process with the bottom two rows, we can work out that a square is worth 2 more than a triangle.

If a square is 2 more than a triangle and a hexagon is 1 more, then a square must be 1 more than a hexagon. The rightmost row is worth 22 and consists of 2 circles, a triangle and a square, and the leftmost one is 2 circles, a triangle and a hexagon. Because a hexagon is worth 1 less than a square, the leftmost row must be worth 1 less and is therefore worth 21.
Some people used algebra. Natalie from Bangkok Patana School and Adithya from Hymers College in the UK used algebra starting from the bottom two rows. This is Natalie's work:
We see the two last rows at the bottom, which clearly contain the same number of circles, except for the triangle and the square. We also understand the value of the two rows; 18 and 20. Therefore, because the difference between between a triangle and a square is 2, the square is 2 greater than the triangle.
We can suppose that 3circles+1square=20. We then substitute the shapes by variables; the circle=$c$, and the square=$s$. Thus, the equation is now $3c+s=20$. For the second equation, the triangle=$t$. Therefore, the equation would be: $3c+t=18$.
In the first equation, we know that $s=t+2.$ Therefore, we can substitute the value of $s$ in terms of $t$ and a constant into the equation. $3c+s=20$ becomes: $3c+t+2=20.$
When we simplify the equation, we want to have like terms on the right side of the equal sign, so $t=18-3c.$
Now, by using the second column from the left side of the table, we can find the solution. We know that $s=t+2.$ In this column, however, there are 3 squares and 1 triangle. [To express 3 squares, we] multiply $3(t+2)$ and get $3t+6$
[So 3 squares + 1 triangle = 30 becomes] $30=3t+6+t,$ we then simplify the equation.
$4t+6=30$
Subtract 6 from the left and right side, we get $4t+6-6=30-6$ OR $4t=24$
Finally, to isolate $t,$ we divide $4t$ by $4$ and $24$ by $4.$ Thus, the triangle=6.
Now, to find the value of the circle, we use our previous equation, $t=18-3c$, and substitute the the $t$ by $6.$ Just by simplifying as we were doing, $6=18-3c$, and the circle equals $4.$
Because we know that the $s=t+2$, $s=6+2.$ Therefore, the square=8. Finally, for the hexagon, we can find the 2nd row form the top to have 2 hexagons and 2 squares. If the hexagon=$h,$ then $2h+2s=30$ so $2h+2(8)=30.$
$2h-16=30.$ Thus, the hexagon=7.
For the first column from the left, we have 1triangle+1hexagon+2circles=?
$t=6, h=7, c=4$ so $6+7+2(4)=?\Rightarrow 6+7+8=?$ Thus, the solution to this problem is:
$?=21$
Siddhant from Singapore International School of Mumbai in India, Lauren from Skipton Girls' High School, Eliya, Lauren and Hannah from North London Collegiate Junior in and Oliver from Abingdon School in the UK, Yerin, Prinn and Utkarsh from Bangkok Patana School and Anh Pham and Anh Minh from British Vietnamese International School used algebra starting from image 1. This is Lauren's work (Skipton Girls'):
To calculate this solution, you must first think of the second column and the first row. As you can see, they consist of squares ($s$) and triangles ($t$). To calculate this I did:
Square Triangle (do this after square)
$2s+2t=28$ $2s+2t=28$
$3s+t=30$ $(2\times8)+2t=28$
$s+t=14$ $16+2t=28$
$(3s+t)-(s+t)= 2s$ $2t=12$
$30-14=16$ $t=6$
$2s=16$
$s=8$
After calculating this you can now move on to the bottom two rows. To do this you use substitution (like you did to calculate the triangle). The circles($c$) are the ones we want to find out. You do the steps as follows (there are several ways to do this so I will just show 2 of them):
$3c+t=18$ $3c+s=20$
$3c+6=18$ Or $3c+8=20$
$3c=12$ $3c=12$
$c=4$ $c=4$
Now that we have calculated the circles, squares and triangles, we can now move on to calculating the hexagons ($h$). There are a few ways to do this and I will show a few possibilities:
$2h+2s=30$ $s+h+2c=23$
$2h+ (2\times8) =30$ $8+h+(2\times4)=23$
$2h+ 16=30$ Or $8+h+8=23$
$2h=14$ $h+16=23$
$h=7$ $h=7$
Finally, we can find out what that mystery number is. We simply use substitution again to calculate it. We do as follows:
$t+h+2c=?$
$6+7+(2\times4)=?$
$6+7+8=?$
$21=?$
Teachers' Resources
Why do this problem?
This problem provides a good challenge in reasoning, working with multiple unknowns. There are issues of redundancy to think about in the provision of too much information.
Students often get stuck when working on mathematical problems. The focus on multiple methods of solving this problem redirects students' attention away from the negative feelings of being stuck and towards the excitement of realising there are many different approaches. This helps students to develop a more resilient mindset when faced with new mathematical situations.
This is a pre-algebra task that can introduce students to the sort of manipulations that can be used to solve simultaneous equations.
Possible approach
Show the grid below, or hand out this worksheet, or display this slide.
"Each symbol has a numerical value. The total for the symbols is written at the end of each row and column."
"Can you find the missing total that should go where the question mark has been put?"
"This is a really interesting problem because it can be solved in lots of different ways. Can you find more than one way to do it?"

"There's a lot of information in the grid, so you had to make some choices about what to focus on first. Each image on the worksheet draws your attention to particular parts of the grid. What can you deduce from each? How can each help you to solve the problem?"
We've set out the worksheet so if you don't want everyone to work on every image, you can give half the class the odd numbered images and half the class the even numbered images.
In pairs or small groups, you could either have the whole pair/group work on each image together, or suggest that each student focuses on one image and then explains it to the rest of the group. Either way, the students will share their interpretations of the images, support each others' understanding and practise explaining their reasoning.
"In a while, I'm going to invite you up to the board to present your favourite method as a completed solution, so be ready to explain every part of your thinking clearly, and to justify why it is your preferred approach."
Here are some prompts that could be offered to students working on the different approaches if they get stuck:
"If you could work out the value of the square/hexagon/circle/triangle, how could you then work out the value of the triangle/circle/hexagon/square?"
"What can you deduce by comparing the bottom two rows?"
Finish off by inviting students to the board to share the completed methods, together with any other methods they thought of for themselves.
The same techniques can be applied to the problems generated by the interactivity in Fruity Totals
Possible support
Students could work in pairs to make sense of the different methods.
The problem could be solved by trial and improvement, so suggest students choose a value for a particular shape and explore the consequences.
Possible extension
Can students work out how much information is necessary to solve the Fruity Totals problems uniquely, and identify redundant information?
