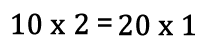Multiply Multiples 1
Can you complete this calculation by filling in the missing numbers? In how many different ways can you do it?
Problem
Multiply Multiples 1 printable sheet
In this calculation, each line represents a missing digit:
$\_0\times\_=\_0\times\_$
One possible solution is:
$10\times2=20\times1$
Can you work out some different ways to balance the equation?
Getting Started
Remember the relationship between 'one times' and 'ten times' a number. For example, 5 x 1 = 5 and 5 x 10 = 50.
You could begin by making both sides of the equation equal to 10, then 20, then 30 and so on.
Is there more than one way of completing the equation for each total? Can any of them be made in lots of different ways?
Teachers' Resources
Why do this activity?
This problem provides the children with an opportunity to practise multiplying a single digit number by a multiple of 10. It also reinforces learning about equations being balanced and may lead to conversations about common factors. It encourages children to record their results, notice patterns and make predictions.
Possible approach
It might be good to let the class explore the problem first before trying to encourage systematic working. The class will hopefully discover issues such as 60 x 1 = 60 x 1 (does this count?!) and 20 x 6 = 30 x 4 = 40 x 3 = 60 x 2 (where there is more than one option). It may be appropriate to then discuss how the class is going to record solutions.
Working systematically might involve starting with the lowest values possible: 10 x 1 = 10 x 1. With 10 on each side of the equals sign, can this be made in any other way? Decide as a class if this example actually counts as both sides of the equation are identical. Then move on to 10 x 2 = 20 x 1. Is there another way of making 20? Then try 10 x 3, 10 x 4 and so on.
Alternatively, you might encourage the class to work through all of the options for 10x and then move on to 20 x 1, 20 x 2, 20 x 3, ...
Organising results according to how many ways in which the equation can be balanced will support the children in noticing patterns and making conjectures.
Some children may move onto the extension tasks (below).
Key questions
Is there another way of balancing the equation? How many ways are there?
Can you use your knowledge of multiplication facts to help you?
Possible extensions
Extension 1: Can you explain why there is sometimes just one way of balancing the equation and on other occasions there are lots of ways of doing it? What do you notice about the numbers?
Extension 2: Have a go at Multiply Multiples 2 for a similar activity multiplying a single digit number by a multiple of 100.
Possible support
Some children may benefit from using Diennes (base 10) apparatus and physically making the amounts. For example, 120 (12 tens) can be organised as 60 x 2, 40 x 3, 30 x 4 and 20 x 6.
Children may be provided with multiplication grids or calculators as appropriate.