Spelling Circle
Problem
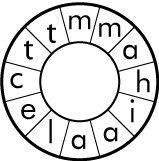
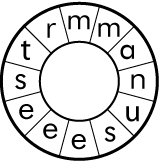
A word is hidden inside each of the circles below. To find the words, start at the letter in the $12$ o'clock position. Then count around a certain number of spaces to find the second letter of the word, then the same number of spaces to find the third letter and so on. It is up to you to figure out how many spaces you need to move each time.
What are the words? How many spaces did you have to move for each letter?
Was it the same number of moves for the two different words?
Try putting your own $12$ letter words in to the circles below. It may seem easy but you might have some difficulties. 'Difficulties' could be a $12$ letter word you use!

Getting Started
Where do you find the first letter? What could the next letter be? And the next?
When you're using your own word, what happens if you put the letters in every second space ... every third space ... every fourth space?
Can you explain why?
Student Solutions
This problem encouraged a huge number of responses. There were different strategies used to solve the problem and many suggestions for other words that could be used to make a spelling circle.
Chen used the guess and check method for problem solving. Chen explains:
I moved randomly ... which eventually led me to the answer.
This can work quite well, but sometimes you have a hunch there is a method or piece of information that will help you. This happened withCaroline, Gabriella, Hanna, Natalie and Rebecca all from The Mount School:
We think it has something to do with $5$ and $7$ not going into $12$.
In fact as the members of Burgoyne Maths Club wrote:
We think that the rule is that if you use factors you go back to where you started and the same thing happens with multiples. The number of spaces you move must NOT be a FACTOR or a MULTIPLE of the SIZE of the CIRCLE.Thomas , Robert and Keiichi from Moorfield Junior School used what they know about multiples:
We got rid of the multiples of twelve because (when we counted spaces we) would have kept on going to the same spaces/letters all the time.
Richard and Luke , also from Moorfield, used the same method:
First we discarded $1$, $2$, $3$, $4$, $6$ and $12$. Then we knew we had six numbers left, so we counted in $5$s round the circle.
Did counting in fives work for the second circle? Christopher , Chris and James found five didn't work and they:
... decided to count on in sevens because it is not a multiple of twelve.
All of the people who sent in their solutions agreed with these boys.
But was there a second solution? Ruth , a pupil at Balderstone Primary School in Blackburn, wrote that she had found five and seven worked but having tried other numbers Ruth reports:
We couldn't do it any other way.
Thank you for your solutions, explanations and willingness to be mathematical problem solvers: Adam , Elliot , Anthony , Steve , Matt T , Matt B , Hanah , Emma and Joanne (Phew!) all from Moorfield Junior School. Chris , Carla , Georgia and Thomas (who cleverly made a spelling circle using the name of the school, Tattingstones). Also, well done to Zoe of Eastbury Farm School in Northwood.
Oh yes, so what were the words? Over to Ruth :
The first one is MATHEMATICAL counting in fives
The second one is MEASUREMENTS counting in sevens.
Here are some words sent in by the readers above. Put the letters to put into a twelve-section circle with the first letter in the $12$ o'clock position and see if you can discover what they are.
I, C, T, I, R, N, E, N, T, E,O, S (It's a word out of a maths
dictionary)
D, A, O, E, D, O, H, N, C, R, D, E
I, U, D, L, V, Y, D, N, A ,E, L, I
G, H, O, C, R, L, P, E, I, G, A, A
These final ones are the same word but using a different ** in
each case.
D, C, E, F, L, I, C, S, I, T, F, U
D, L, F, I, I, S, U, I, T, F, E, C
Here are series of possible words from Burgoyne Maths Club :
| Size of circle | Arrangement of letters starting at 12 o'clock going clockwise |
Number of spaces | Answer |
|---|---|---|---|
| 7 | HANXOEG | 5 | HEXAGON |
| 10 | DOCONADSGE | 3 | DODECAGONS |
| 9 | DCNEODGOA | 7 | DODECAGON |
| 5 | OODVI | 3 | OVOID |
| 15 | TNAIRGRSIUPMALR | 4 | TRIANGULAR PRISM |
| 12 | DEDRCNHOEEOA | 7or19 | DODECAHEDRON |
Let me leave you with this question: If the spelling circles don't work with multiples of $12$, will they also work when counting by $8$, $9$, $10$ or $11$? After all, they are not factors of $12$.
