This puzzling sweet shop
Problem
Ruby went into the sweet shop with 10¢ to spend.
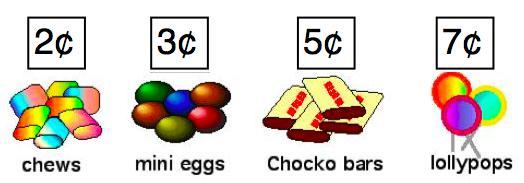
There were cola bottles for 2¢, mini eggs for 3¢, marshmallow twists for 5¢ and lollipops for 7¢.
| 2¢ | 3¢ | 5¢ | 7¢ |
Image
Cola bottles |
Image
Mini eggs |
Image
Marshmallow twists |
Image
Lollipops |
What could she buy if she wanted to spend all her money?
----------
Leo, Kai, Sara and Harry went into the shop too. They each had 20¢ to spend and they all spent all of their money.
Leo bought at least one of each kind of sweet. Which one did he have two of?
Kai spent his money on just one kind of sweet, but he does not like cola bottles. Which sweets did he buy?
Sara bought the same number of sweets as Kai but she had 3 different kinds. Which sweets did she buy?
Harry chose 8 sweets. What could he have bought?
(If you want to do this using UK pence instead go here 
Getting Started
Think of ways that $10$ and $20$ can be divided up.
Student Solutions
These solutions are for a previous version of this task, where cola bottles were called chews and marshmallow twists were chocko bars instead.
Kaylee J sent us answers to the Puzzling Sweet Shop problem:
Rosie can buy:
One lollypop and one mini egg.
One chocko bar, one mini egg and one chew.
Are there any other combinations of sweets Rosie can buy? Let us know if you think there are.
Kaylee goes on to answer the rest of the questions:
Leo bought two mini eggs. I know this because this is the only combination of sweets which add up to 20c where she bought at least one set of every sweet.
Kai bought 4 chocko bars. I know this because it is the only sweet that has a price that can divide into 20c exactly where chews are not included.
Sara bought 2 chocko bars, one lollypop and a mini egg.
Harry bought one chocko bar, one mini egg and 6 chews.
There may be some other sweets that Henry could buy too. Jessica suggests 4 chews and 4 mini eggs. I wonder if there are any other combinations?
Teachers' Resources
This Puzzling Sweet Shop
Ruby went into the sweet shop with 10 ¢ to spend.
There were chews for 2 ¢, mini eggs for 3 ¢, Chocko bars for 5 ¢ and lollypops for 7 ¢.
What could she buy if she wanted to spend all her money?
----------
Leo, Kai, Sara and Harry went into the shop too. They each had 20 ¢ to spend and they all spent all of their money.
Leo bought at least one of each kind of sweet. Which one did he have two of?
Kai spent his money on just one kind of sweet, but he does not like chews. Which sweets did he buy?
Sara bought the same number of sweets as Kai but she had 3 different kinds. Which sweets did she buy?
Harry chose 8 sweets. What could he have bought?
(If you want to do this using UK pence instead go here
Why do this problem?
This problem presents learners with a pleasant and familiar situation in which to explore aspects of the four operations. It also relies on finding all possibilities so can be used to focus on working systematically.
Possible approach
It might be helpful just to have the image displayed, or for you to redraw a similar image, and for you to ask the questions orally rather than children having to read from the screen.
Begin with Ruby and suggest children work in pairs to find possible solutions. After a minute or so, you might like to take a couple of answers and then emphasise you'd like to know all the combinations that Ruby could have bought. In a mini-plenary invite learners to share different ways of going about finding them all and draw attention to those who have developed a system, for example starting with the most expensive sweet (a lollipop) and seeing what could be bought with that; then looking at the next most expensive and finding the combinations which could go with it etc. At this stage, you may also want to highlight some good ways of recording that children have come up with.
Once you have explained about the other four children, you could jot a reminder of how they each spent their 20¢ on the board and leave the class to explore possibilities this time. When you bring their ideas together, you may want to praise those who have developed systematic ways of working based on the earlier discussions and those who explain their reasoning clearly.
Key questions
Could all the sweets be the same?
How do you know you have all the possibilities?
Possible extension
Learners could investigate how other amounts of money perhaps between 10¢ and 20¢, could be spent exactly.
Possible support
It could be useful for children to have objects to represent the sweets, for example coloured counters.