You may also like

problem icon

Cut it Out

Can you dissect an equilateral triangle into 6 smaller ones? What number of smaller equilateral triangles is it NOT possible to dissect a larger equilateral triangle into?

problem icon

Tessellating Transformations

Can you find out how the 6-triangle shape is transformed in these tessellations? Will the tessellations go on for ever? Why or why not?

problem icon

Triangular Hexagons

Investigate these hexagons drawn from different sized equilateral triangles.

Tri-five

Stage: 2 Challenge Level: Challenge Level:1

Finding the best solution for this problem depended on thinking very carefully about what was meant by DIFFERENT ways of arranging the five triangles. For example: Christine (Malborough School) explained:

There is only one shape from the hexagon group because when this shape is rotated it looks like different shapes but it is just one basic shape.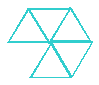

1

As Sophie said:

There were four different shapes using all five equilateral triangles, without rotating the shapes. The shapes I made were:
One was long and thin, but was not a perfect line because it had three triangles on one side and two triangles on the top side.
The second shape had four triangles sloping upwards, and one triangle on the side of it.
The third shape was a big triangle with a smaller triangle on the side of the top one.
And the fourth shape was shaped in the way of a croissant, and had three triangles in a row, and two on top of the two end triangles.

Leyla (Private IRMAK Primary School, Istanbul, Turkey) sent in drawings of the four ways:


2

Merve (Private IRMAK Primary School, Istanbul, Turkey) agreed with this set of four shapes too.


Caroline and Rebecca (The Mount School, York) also realised that some shapes they found were really the same as others if you turned them around or flipped them over:

We found six different ones, but two of these are reflections in a way, so maybe it's only four.

Kirstine (Tattingstone School) also saw how to group some 'variations' of the same shape together. However, if you decided to think about each position of the shape as being different, then there would be many shapes in your solution.

Ece (Private Irmak Primary School) found $18$ shapes. Do think there are any more?

Christopher (Tattingstone School) found two more variations of the straight line. Well done to everyone else who sent in some shapes.


3
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.